- Intro
- Review papers
- DP methods
- Automata methods
- Suffix array methods
- Other
- TODO
- TODO
- Chang and Lampe (1992)
- Baeza-Yates 1989 Improved string searching
- Baeza-Yates 1989 Efficient text searching (PhD thesis)
- Baeza-Yates 1989 string searching algorithms revisited
- Baeza-Yates and Perleberg (1996)
- Baeza-Yates and Navarro (1996)
- Baeza-Yates and G. Navarro (1999)
- Navarro and Raffinot (2000)
- Fredriksson (2003)
- Baeza-Yates and Navarro (2004)
- Hyyrö and Navarro (2004)
- Fredriksson and Navarro (2003)
- Fredriksson and Navarro (2004)
- Fredriksson and Grabowski (2005)
- Farrar (2006)
- Hyyrö (2008b)
- Benson, Hernandez, and Loving (2013)
- Setyorini et al. (2017)
- Goenka et al. (2020)
- Mishin, Berezun, and Tiskin (2021)
- Loving, Hernandez, and Benson (2014)
- (NO_ITEM_DATA:X)
- TODO
\[ \newcommand{\ceil}[1]{\lceil#1\rceil} \newcommand{\floor}[1]{\lfloor#1\rfloor} \]
Intro
This note summarizes some papers I was reading while investigating this history of bitpacking methods such as Myers (1999). This post was sparked by Loving, Hernandez, and Benson (2014), which cites many works of Hyyrö. I then discovered that in fact Hyyrö wrote many papers on bitpacking methods. Then while reading these, I also found many citations to (approximate) string searching algorithms (aka semi-global alignment, aka (approximate) pattern matching). In particular Baeza-Yates and Navarro wrote many papers on this topic. Some of those use bit-packing while others don’t. Paper also differ in the distance metric they use (/mismatches (Hamming distance), matches (LCS distance), differences (edit distance), indel distance), and which approach they use (automata or DP); see the corresponding sections.
For the classic DP bit-packing methods like Myers (1999), see DP methods.
In the semi-global setting, the convention is that the (short) pattern has length \(m\) (sometimes assumed to be at most the word size \(w\)), and that the text has length \(n\gg m\). Semi-global alignment is also called (approximate) string matching. For global alignment, typically \(m\sim n\). Throughout this post, I assume the alphabet size is constant.
Generally, there is a distinction between practical algorithms and theoretical algorithms. The latter often requiring e.g. a suffix array for \(O(m)\) runtime and hence being slower in practice than a \(O(m^2)\) DP-based implementation.
PDFs of some papers listed here are hard to find. I’m happy to share them on request.
Review papers
- Chang and Lampe (1992) “Theoretical and Empirical Comparisons of Approximate String Matching Algorithms”
- Very comprehensive 10 page comparison of theory of many early
algorithms, and analyses them on random strings. Introduces diagonal transition term.
TODO: Read this carefully.

Figure 1: Summary of Chang and Lampe (1992). Such a nice table. Empirical runtime should be more widespread.
- Baeza-Yates (1992) “Text-Retrieval: Theory and Practice”
- 15 page review, but focuses on a slightly different topic.
- Navarro (2001) “A Guided Tour to Approximate String Matching”
- 50 page long review paper. Useful as reference but long to read.
- Navarro and Raffinot (2002) “Flexible Pattern Matching in Strings”
- 200 page book. I didn’t actually read this; it just appeared as citation.
DP methods
LCS
Allison and Dix (1986)
“A Bit-String Longest-Common-Subsequence Algorithm”

Figure 2: Formula of Allison and Dix (1986), as shown by Hyyrö (2004).
- First bit-parallel LCS; well written
- \(O(n\ceil{m/w})\) LCS
- Contours
- Bit-profile, called Alphabet strings
- Encoding: bits of \(row_i\) store horizontal differences (in \(\{0,1\}\)) within rows.
- \(6\) operations per word: \[row_i = x\land ((x-((row_{i-1}\ll 1)|1))) \neq x),\] where \(x=row_{i-1} \lor b_i\).
- equivalently (Hyyrö 2004) \[row_i = x\land (\sim(x-((row_{i-1}\ll 1)|1))).\]
- The \(-\) and \(\ll\) have to be carried through the entire row if it consists of multiple words.
- The \(|1\) can be absorbed into the carry-through instructions (Hyyrö 2004).
Crochemore et al. (2001)
“A Fast and Practical Bit-Vector Algorithm for the Longest Common Subsequence Problem”
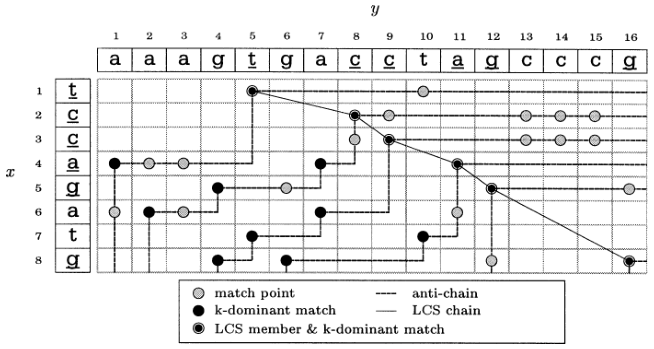
Figure 3: Crochemore et al. (2001) LCS contours
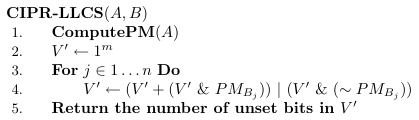
Figure 4: Formula of Crochemore et al. (2001), as shown by Hyyrö (2004).
- \(O(n\ceil{m/w})\) LCS, like Allison and Dix (1986)
- \(4\) instead of \(5\) bit-wise operations.
- Contours
- Bit-profile \(M[y_j]\) for $j$th char of \(y\), and \(M’[y_j]\) is its negation.
- Encoding: \(\Delta L’_j\) is the negation of the differences in a column, i.e. \(1\) when two consecutive values are the same.
- \(4\) operations, but \(2\) table accesses: \[\Delta L’_{j+1} = (\Delta L’_j + (\Delta L’_j \land M[y_j])) \lor (\Delta L’_j \land M’[y_j])\]
- In practice computing \(M’[y_j] = \sim M[y_j]\) on the fly is faster (Hyyrö 2004).
- Only the \(+\) has to be carried through the entire row if it consists of multiple words.
Hyyrö (2004)
“Bit-Parallel Lcs-Length Computation Revisited”

Figure 5: Formula of Hyyrö (2004).
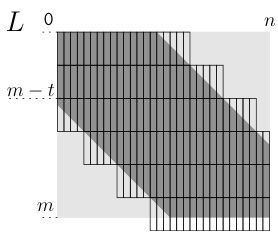
Figure 6: Tiling the restricted grid of Hyyrö (2004).
Reviews Allison and Dix (1986) and Crochemore et al. (2001); very well written.
\(O(n \ceil{m/w})\) LCS, or \(O(n\ceil{d/w})\) LCS based on Ukkonen’s band doubling for simple edit distance, i.e. edit distance without substitutions.
Bit-profile \(PM_\lambda\) called pattern matching bit-vectors or match vector for \(\lambda\in \Sigma\).
Uses same encoding as Crochemore et al. (2001), but calls it \(V’\).
One less operation/table lookup less than Crochemore et al. (2001):
\begin{align*} U &= V’ \& PM_{B_j}\\ V’ &= (V’ + U) | (V’ - U) \end{align*}
Two carry-through operations between words.
Implementation is column-wise.
\(11\) operations overhead in the loop to do carry and looping and such.
Measured runtime differences between implementations are small (\(<20\%\)) and likely depend mostly on how well the compiler optimizes each version.
Figure 6 shows the tiling when given a lower bound on LCS (resp. upper bound on simple edit distance).
Hyyrö (2017)
“Mining Bit-Parallel Lcs-Length Algorithms”
- Using an exhaustive search, it is shown that under reasonable assumptions LCS can not be solved using \(3\) binary operations.
- A total of \(5\) algorithms using \(4\) operations are found.

Figure 7: The five 4-operation LCS algorithms found by Hyyrö (2017).
Edit distance
Wright (1994)
“Approximate String Matching Using Withinword Parallelism”
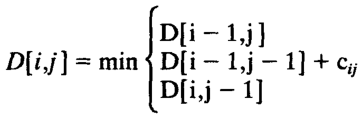
Figure 8: DP of Wright (1994). I don’t get it.
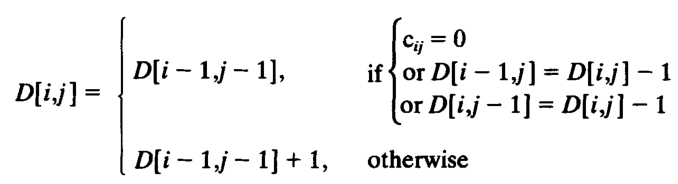
Figure 9: Modified DP of Wright (1994). This one is self referential… I get it even less.
- \(O(nm/w)\) antidiagonal proccessing of the DP-matrix using bitpacking on \(\mod 4\) values, as in Lipton and Lopresti (1985) (see Lipton and Lopresti (1985) below).
- This is implemented without \(\min\) operations by using equalities instead.
- Uses \(3\) bits per value: one padding for carry to avoid overflowing into the next state.
- I have some confusions about this paper:
Myers (1999)
“A Fast Bit-Vector Algorithm for Approximate String Matching Based on Dynamic Programming”

Figure 10: Myers (1999) bitpacking algorithm when (mleq w).
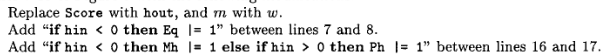
Figure 11: Myers (1999) bitpacking algorithm modification for (m>w).
- \(O(n\ceil{m/w})\) Edit distance
- Semi-global alignment. For long patterns, the technique of Wu, Manber, and Myers (1996) is used for \(O(n \ceil{k/w})\) expected time.
- Bit-profile \(Peq\)
- Bitpacking; \(15\) operations assuming horizontal input deltas are \(0\) and no horizontal output deltas are needed.
- Encoding:
Ph, Mh, Pv, Mvindicators store whether Horizontal/Vertical differences are Plus \(1\) or Minus \(1\). Horizontal deltas are standalone bits, and vertical deltas are packed. - Core observation: there is a carry effect when there are specific long runs of ones. This is similar to the carry of addition.
- Core component are \(Xv = Eq | (\Delta v_{in} = M)\) and \(Xh = Eq | (\Delta h_{in} = M)\)
- Between blocks in a column, \(h_{out}\) is computed and carried over, instead of carrying the addition and two shift operations individually.
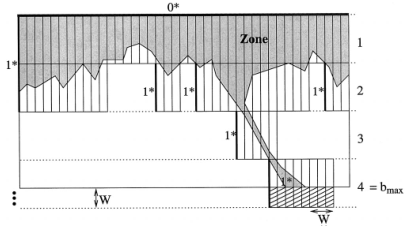
Figure 12: Myers (1999) block based algorithm for semi-global alignment.
Hyyrö (2001)
Explaining and Extending the Bit-Parallel Algorithm of Myers

Figure 13: Hyyrö (2001) bitpacking algorithm when (mleq w).
- \(O(n\ceil{m/w})\) edit distance, or \(O(n \ceil{k/w})\) expected time semi-global alignment.
- Equivalent but slightly different bit algorithm than Myers (1999); core component is \(D0 = Xv | Xh\).
- Also shows how to do transpositions (Damerau 1964).
- Good introduction and exposition.
- Uses \(15\) operations (\(HP_j\ll 1\) can be reused); same as Myers (1999) \(15\) operations.
Hyyrö (2003)
“A Bit-Vector Algorithm for Computing Levenshtein and Damerau Edit Distances”
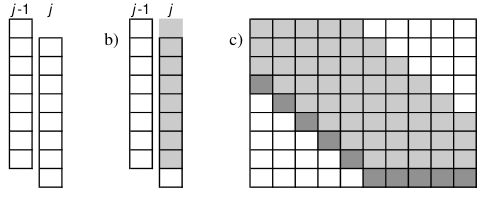
Figure 14: Hyyrö (2003) tiles bit-vectors diagonally.
- \(O(\ceil{d/w}m)\) edit distance (optionally with transpositions).
- Merges bitpacking (Myers 1999) with band doubling (Ukkonen 1985a).
- Introduces diagonal tiling, to better match the statically banded region of (Ukkonen 1985a).
- Diagonal tiling allows the removal of some shifts (i.e. in the last two lines of Figure 13, but adds a shift in the opposite direction for \(D0\). This introduces a ‘‘backwards’’ dependency on the vector below-left of it that is not present with rectangular tiling.
- The pattern-match vector \(PM_j\) is shifted to correct for the unaligned reads.
- Includes a comparison with band doubling and bitpacking algorithms of Ukkonen and Myers. Surprisingly, Ukkonen’s algorithm that computes values by increasing distance (i.e. Dijkstra) is reported as faster that the band doubling algorithm, even though Dijkstra is usually considered slow. Sadly no code is provided.
Hyyrö, Fredriksson, and Navarro (2004)
“Increased Bit-Parallelism for Approximate String Matching”
- For short patterns, when \(m \ll w\), the \(O(\ceil{m/w}n)\) runtime wastes many bits of each word.
- They show how to search for \(\floor{w/m}\) patterns simultaneously, by packing multiple patterns in a single word, for \(O(\ceil{r/\floor{w/m}}n)\) total time for \(r\) patterns.
- They show how to search for a single pattern in \(O(n/\floor{w/m})\).
- They apply the cut-off techniques to improve this to \(O(\ceil{r/\floor{w/k}}n)\) and \(O(n/\floor{w/k})\) expected time respectively when at most \(k\) errors are allowed.
- To avoid interference when adding/shifting, the most significant bit of each pattern is set to \(0\) beforehand.
- The score at each position is tracked by packing $m$-bit counters into a single word, together with adding some offset to make detection of \(>k\) values easy.
- To efficiently search a single pattern, the text is split into \(r:=\floor{w/m}\) chunks. Then, instead of searching multiple patterns against the same text, one can search the same pattern against different texts by or-ing together the bit-profile of the different text characters.
Hyyrö, Fredriksson, and Navarro (2005)
“Increased Bit-Parallelism for Approximate and Multiple String Matching”
This is the journal version of the conference paper Hyyrö, Fredriksson, and Navarro (2004) above, and includes a few more results.
It applies the ideas to multiple exact string matching, searching \(r\) patterns in average time \(O(\ceil{r \log_\sigma w/w}n)\), by searching the first \(\ceil{\log_\sigma w}\) characters of each pattern in parallel.
It applies to one-vs-all edit distance, where multiple patterns are packed in a word, and similar for LCS.
Hyyrö and Navarro (2002)
“Faster Bit-Parallel Approximate String Matching”
This is the conference paper of the journal paper Hyyrö and Navarro (2004) below.
Hyyrö and Navarro (2006)
“Bit-Parallel Computation of Local Similarity Score Matrices with Unitary Weights”
Solves local alignment using bitpacking in \(O(mn \log \min(m,n,w)/w)\) time.
Contains a quite nice introduction on global vs semi-global vs local alignment.
Local similarity computation needs a somewhat different arrangement and, curiously, it seems not expressible using the distance model, but just the score model.
Score model \(+1\) for match, \(-1\) for substitution and indel.
Difficulties:
- Absolute scores must be known to do \(\max(0, \cdot)\).
- Cells can differ by \(2\).
Introduces witnesses: Every \(Q = O(\log \min(m,n))\) rows the absolute value is stored and tracked (using bitpacking). For each column, all absolute values are then compared against \(0\) and \(k\) by taking the \(m/Q\) known values and incrementally shifting these down using the know vertical differences.
The resulting algorithm is a beast with \(21\) lines of code each containing multiple bit operations.
Indel distance
This is problem of finding all matches of a pattern in a string with indel distance at most \(k\), where only indels (insertions and deletions) are allowed, and substitutions are not allowed (or equivalently, they have cost \(2\)). Note that in the semi-global alignment case this is not exactly equivalent to LCS.
Lipton and Lopresti (1985)
“A Systolic Array for Rapid String Comparison”
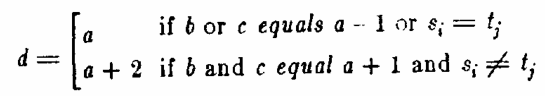
Figure 15: DP of Lipton and Lopresti (1985).
- Introduces recurrence on the DP matrix using mod 4 arithmetic.
- Parallel over antidiagonals
- Note: this has substitution cost \(2\), so it’s actually using indel distance.
Hyyrö, Pinzon, and Shinohara (2005a)
“Fast Bit-Vector Algorithms for Approximate String Matching under Indel Distance”
Modifies existing algorithms for indel-distance.
Myers (1999) requires modifications, because along diagonals values can now increase by \(2\) instead of only \(0\) and \(1\). Runtime is \(O(\ceil{m/w}n)\).
Wu and Manber (1992) and Baeza-Yates and G. Navarro (1999) are modified by simply removing one case from the DP recurrence. Runtimes are \(O(k\ceil{m/w}n)\) and \(O(\ceil{(k+2)(m-k)/w}n)\) respectively, and are faster than Myers (1999) for small \(k\) and small \(m\).
The recurrence for \(D\) in the first paragraph of the introduction (and also later in the introduction) seems to be missing some \(+1\) terms for indels. Or maybe I’m missing something?
Hyyrö, Pinzon, and Shinohara (2005b)
“New Bit-Parallel Indel-Distance Algorithm”
- Improves the runtime of the indel-distance variant of Myers (1999) introduced in (Hyyrö, Pinzon, and Shinohara 2005a) from \(26\) operations to \(21\) operations.
- The overall speedup was \(24.5\%\), more than the instructions savings of \(19\%\).
- Has a much clearer presentation than the previous paper.
Automata methods
These methods are based on automata (as opposed to a DP matrix). This means that instead of storing the distance to a state, they for instance indicate whether the state can be reached with cost \(d\) in a bit vector/matrix \(R^d\). Nevertheless, some of these methods seem very closely related to DP based methods, and this categorisation is not absolute. Rather, I just needed some way to separate out papers a bit.
This category also includes e.g. the Knuth-Morris-Pratt algorithm for linear time exact string matching.
Hamming distance
Landau and Vishkin (1986)
“Efficient String Matching with K Mismatches”
- \(O(k(m\log m+n))\) approximate string matching under Hamming distance.
- Constructs some kind of jumplists with mismatches to quickly determine the new number of mismatches after shifting the pattern. (But I did not read or understand in detail.)
Baeza-Yates and Gonnet (1992)
“A New Approach to Text Searching”
\(O(mn/w)\) string search under Hamming distance; one of the first uses of bitpacking.
- Shift-add algorithm works by counting the number of mismatches along diagonals of the \(m\times n\) matrix.
Already submitted in 1989.
Supposedly builds on theory of finite automata, but seems like a pretty direct algorithm to me.
Extends to matching with character classes, but still only does Hamming distance.
\(O(nm \log k/w)\) when counting up to $k$-mismatches (Hamming distance), by storing each count in \(\log k\) bits (instead of a single match/mismatch bit).
Multiple exact string matching in \(O(\ceil{m_{sum}/w}n)\) time.
side note: 3 column layout is terrible – too much scrolling up and down.
TODO Baeza-Yates and Gonnet (1994)
“Fast String Matching with Mismatches”
Edit distance
Ukkonen (1985b)
“Finding Approximate Patterns in Strings”
When the pattern length \(m\) is small, one can build an automaton where states correspond to columns of the DP matrix, and transitions to parsing a character of the text.
- This gives \(O(n)\) processing time once the automaton has been built.
- There can be up to \(K=\min(3^m, 2^t \cdot |\Sigma|^t\cdot m^{t+1})\) different columns, meaning \(O(m\cdot |\Sigma|\cdot K)\) precomputation can be very slow.
- All states can be found from the initial state by BFS/DFS.
- Not practical.
Landau and Vishkin (1985)
“Efficient String Matching in the Presence of Errors”
Note that Landau and Vishkin (1986) was submitted before this.
Generalizes this earlier paper to edit distance in \(O(m^2 + k^2 n)\) time.
we first build a table based on analysis of the pattern. Then, we examine the text from left to right checking possible occurrences with respect to on starting location (in the text) at each iteration.
Like the Hamming distance paper, this seems quite involved and technical.
TODO: read more carefully at some point (although the details do not sound super interesting/relevant).
Landau and Vishkin (1988)
“Fast String Matching with K Differences”
- Builds on Landau and Vishkin (1985) (earlier conference paper).
- \(O(m + k^2 n)\) approximate string search.
Wu and Manber (1992)
Published in same journal issue as Baeza-Yates and Gonnet (1992) and extends it to edit distance.
\(O(nkm/w)\) to find all matches of cost at most \(k\).
- Introduces indicator bit-vectors \(R^d_j[i]\), such that \(R^d\) stores whether there is a path of cost \(d\) to DP state \((i,j)\).
Introduces the partition approach: If \(k\ll m\) errors are allowed, at least one part must match when the pattern is partitioned into pieces of length \(r=\floor{m/(k+1)}\). Thus, one can first do a exact search for multiple patterns, followed by an inexact search around matches.
(TODO: Cite for A*PA)
Solves multiple exact pattern matching by interleaving the (equal length) patterns and shifting left by the number of patterns, instead of by \(1\).
Extends to character classes and wild cards, like Baeza-Yates and Gonnet (1992).
Extends to small integer costs for operations.
For long patterns and \(k>w\), only up to \(w\) errors are considered by default and more is only computed when a good candidate is found.
For regular expressions, nondeterministic finite automaton are using.
agrep: Approximategrep.
Bergeron and Hamel (2002)
“Vector Algorithms for Approximate String Matching”
- Extends (Baeza-Yates and Gonnet 1992) and (Myers 1999) to arbitrary bounded integer weights for edit distance, showing that \(O(c \log c)\) bit vector operations are sufficient per column transition, for \(O(mnc\log( c)/w)\) total runtime.
- Very formal paper – hard to read and understand what is practically going on.
- Does not give an actual algorithm/implementation, nor experiments.
Suffix array methods
Hamming distance
Galil and Giancarlo (1986)
“Improved String Matching with K Mismatches”
- \(O(m+nk)\) for $k$-mismatches string matching
- Uses a suffix array with LCA for \(O(1)\) extension. At each position, simply extend \(k\) times.
Grossi and Luccio (1989)
“Simple and Efficient String Matching with K Mismatches” Based on permutations.
- First finds all occurrences of permutations of the pattern in the text.
- Extend that to find all permutations of the pattern with at most \(k\) mismatches.
- For each match, check if the hamming distance is small.
- Personal remark: it should be possible to extend this to edit distance.
Edit distance
Landau and Vishkin (1989)
“Fast Parallel and Serial Approximate String Matching”
- \(O(nk)\) time approximate string matching under edit distance.
- \(O(\log m + k)\) serial algorithm using \(n\) processors.
- Uses diagonal transition (Ukkonen 1983, 1985a) together with \(O(1)\) extension using a suffix array. (Similar to Galil and Giancarlo (1986).)
Galil and Park (1990)
“An Improved Algorithm for Approximate String Matching”
- \(O(kn)\) approximate string matching with \(k\) differences
- Diagonal transition
- Builds \(O(m^2)\) lookup table for longest-common-prefix between any two suffixes of the pattern.
- Uses reference triples \((u,v,w)\): a maximal substring \(u\dots v\) of the text that equals \((u-w)\dots (v-w)\) of the pattern.
- Using these, diagonals can be extended efficiently.
- TODO: try to understand this better. It sounds interesting, but needs careful reading.
Chang and Lawler (1990)
“Approximate String Matching in Sublinear Expected Time”
Based on suffix trees.
Edit distance in \(O(m)\) space and \(O(nk/m \cdot \log m)\) sublinear expected time on random strings. Worst case \(O(nk)\).
quote:
Previous algorithms require at least \(O(nk)\) time. When \(k\) is a s large as a fraction of \(m\), no substantial progress has been made over \(O(nm)\) dynamic programming.
Twice cites Ukkonen, personal communication :(
Exact matching in sublinear expected time: For positions \(s \in \{m, 2m, 3m, \dots\}\), find all \(j\) such that \(T[s+1, \dots, j]\) is a suffix of the pattern. For random strings, \(j-s > \log(m)\) is not a suffix with high probability, so there are only \(O((n/m) \log m)\) matches in total, each of which is quickly checked.
In the inexact case, we can for each position \(S_j\) in \(T\) query the length \(\ell\) of longest prefix of \(T[S_j, \dots]\) that is a substring of the pattern, and then jump to \(S_{j+1} = S_j + \ell +1\). If \(S_{j+k+2} - S_j \geq m-k\) that means it may be possible to match all \(m\) chars here with at most \(k\) mistakes, in which case an DP-based algorithm can be used for verification.
To obtain sublinear expected time, the text can be partitioned into \((m-k)/2\) chunks, so that any match includes at least one whole region. Then, we can make \(k+1\) maximum jumps from the start of each region. Only if those span the entire region, a match is possible there.
Chang and Lawler (1994)
“Sublinear Approximate String Matching and Biological Applications”
This is the journal version of the conference paper Chang and Lawler (1990). It seems no additional methods are introduced. (Rather, additional applications are shown.)
Other
Some more papers that I downloaded as part of this reading session, but that turned out somewhat unrelated.
Hyyrö (2008a)
Solves the problem of consecutive suffix alignment, where \(A\) is aligned to prefixes of growing suffixes \(B_{j..n}\) for decreasing \(j\). Given an \(O((m+n)n)\) time and \(O(m+n)\) space algorithm, which is the first linear space algorithm.
This can be used when the end position of a match in approximate string matching is known, and the start position needs to be recovered.
The algorithm description looks very technical, and sadly no high-level overview and/or figures are provided, so I did not read this in detail.
Hyyrö, Narisawa, and Inenaga (2010)
“Dynamic Edit Distance Table under a General Weighted Cost Function”
This generalizes Hyyrö (2008a) to non-unit cost weights.
It has a somewhat intuitive explanation of an earlier algorithm of Kim and Park.
TODO
Many citations link to Lecture notes in compute science instead of the original conference. Ideally this is fixed.
TODO
Chang and Lampe (1992)
“Theoretical and Empirical Comparisons of Approximate String Matching Algorithms”
Baeza-Yates 1989 Improved string searching
Baeza-Yates 1989 Efficient text searching (PhD thesis)
Baeza-Yates 1989 string searching algorithms revisited
Baeza-Yates and Perleberg (1996)
“Fast and Practical Approximate String Matching”
Baeza-Yates and Navarro (1996)
“A Faster Algorithm for Approximate String Matching”
Baeza-Yates and G. Navarro (1999)
Navarro and Raffinot (2000)
“Fast and Flexible String Matching by Combining Bit-Parallelism and Suffix Automata”
Fredriksson (2003)
Baeza-Yates and Navarro (2004)
Hyyrö and Navarro (2004)
“Bit-Parallel Witnesses and Their Applications to Approximate String Matching”
- New bitpacking technique building on ABNDM [TODO] and Myers (1999) bitpacking.
- Introduces witnesses: sparse states of the DP matrix from which others can be bounded quickly.
- Improves Myers (1999) as well.
- \(\alpha = k/m\) is called difference ratio.
Fredriksson and Navarro (2003)
“Average-Optimal Multiple Approximate String Matching” This is the conference paper corresponding to the twice as long journal paper Fredriksson and Navarro (2004).
Fredriksson and Navarro (2004)
“Average-Optimal Single and Multiple Approximate String Matching”
Fredriksson and Grabowski (2005)
“Practical and Optimal String Matching”
Farrar (2006)
“Striped Smith–Waterman Speeds Database Searches Six Times over Other Simd Implementations”
Hyyrö (2008b)
“Improving the Bit-Parallel Nfa of Baeza-Yates and Navarro for Approximate String Matching” bit parallel NFA