The supplement (download) of the Loving, Hernandez, and Benson (2014) paper introduces a \(15\) operation version of Myers (1999) bitpacking algorithm, which uses \(16\) operations when modified for edit distance.
I tried implementing it, but it seems to have a bug that I will describe below. The fix is here.
Problem
To recap, this algorithm solves the unit-cost edit distance problem by using bitpacking to compute a \(1\times w\) at a time. As input, it takes
- horizontal differences (each in \(\{-1, 0, +1\}\)) along the top,
- the vertical differences on the left (also in \(\{-1,0,+1\}\)),
- which characters along the top match the character on the left.
It outputs:
- the new horizontal differences along the bottom,
- the new vertical difference on the right.
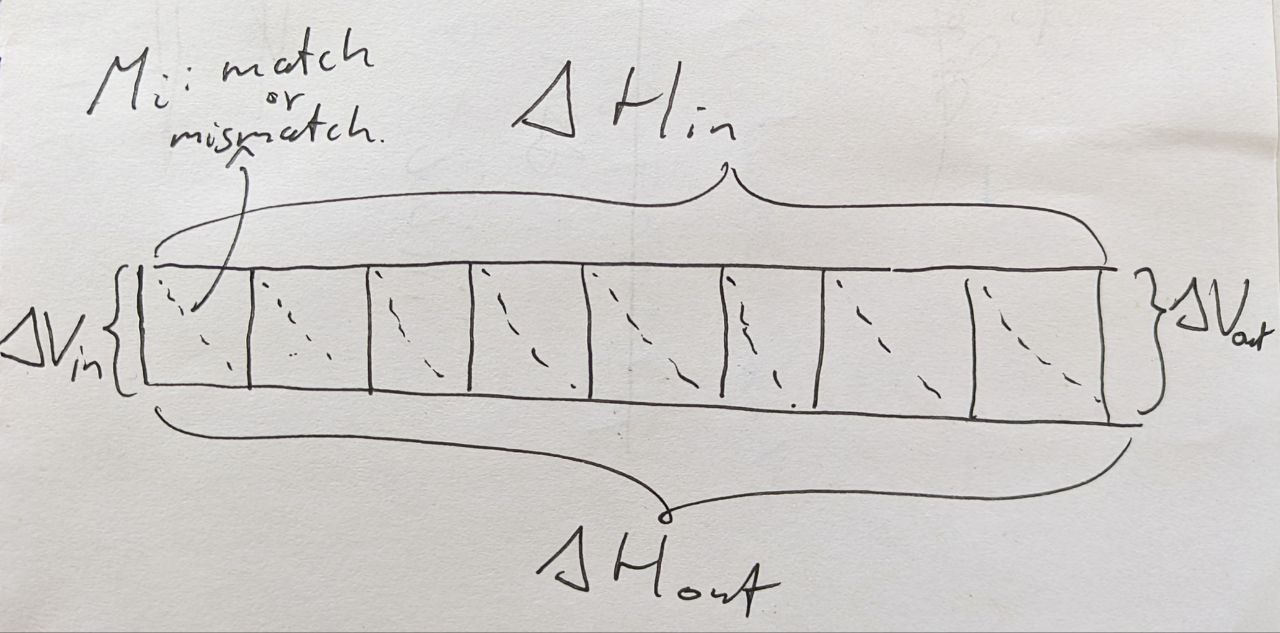
Figure 1: Bitpacking layout of BitPAl, showing a row of (w=8) cells.
Input
- A bitvector \(M\) indicating for \(w\) horizontally adjacent positions whether there is a match. \(M_i = 1\) when the \(i\)’th cell contains a match. I’ll use \(w=8\) here.
- A bitvector \(D\), with \(D_i = 1\) when the horizontal difference along the top of cell \(i\) is Decreasing, i.e. \(-1\).
- A bitvector \(SD\) (\(S|D\) in that paper), with \(SD_i = 1\) when the horizontal difference along the top of cell \(i\) is the Same or Decreasing, i.e. \(0\) or \(-1\).
- The vertical difference on the left is assumed to be \(1\) in case of edit distance.
Example
Consider the following example input:
- All horizontal input differences are \(+1\), i.e. \(\Delta H_in = (+1,+1,\dots,+1)\). This means none are decreasing or the same, so \(D=00000000_2\) and \(SD=00000000_2\) (in binary).
- The vertical input difference is also \(+1\), as already assumed for edit distance.
- There are matches at positions \(2\) and \(5\), so \(M = (0,0,1,0,0,1,0,0) = 00100100_2\).
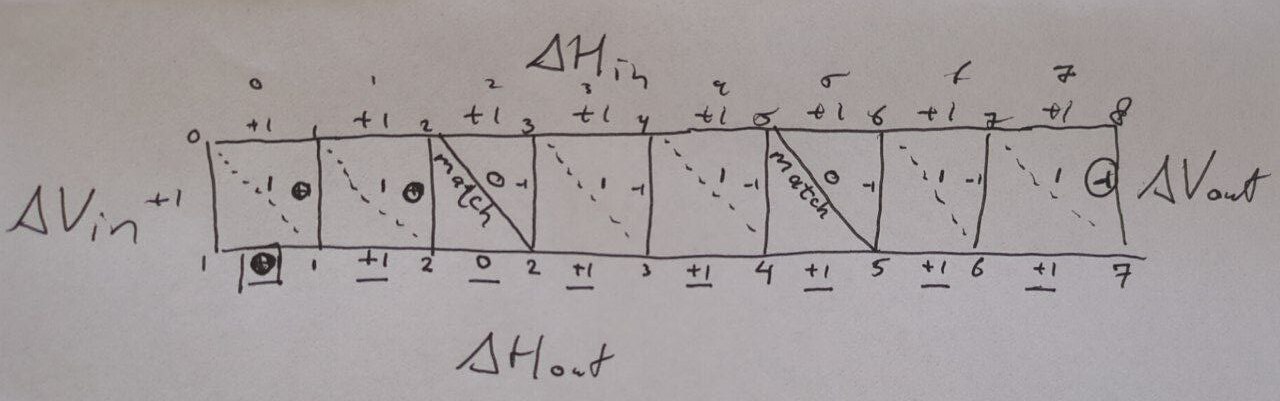
Figure 2: Example with horizontal and vertical input deltas all equal to (1) and some matches (solid diagonal lines).

Figure 3: BitPAl’s algorithm
Working through the example (Figure 2), we see that the output horizontal differences are \((0, 1, 0, 1, 1, 1, 1, 1)\), so we expect \(D = 0\) (no decreases) and \(SD = 00000101_2\) (the first position corresponds to the least significant digit).
Now let’s run through the code.
Note: \(\wedge\) is xor, and \(\&\) is and.
- \(M_m = M|D = 00100100 | 0 = 00100100\)
- \(R_{I|S} = \sim M_m = 11011011\)
- \(notM_I = R_{IS} | SD = R_{IS} | 0 = 11011011\)
- \(R_{I|S}orS = notM_I \wedge D = notM_I \wedge 0 = 11011011\)
- \(Sum = notM_I + SD = 11011011 + 0 = 11011011\)
- \(MaskSum = Sum \& R_{I|S} = 11011011 \& 11011011 = 11011011\)
- \(V_0 = MaskSum \wedge R_{I|S}orS = 11011011\)
- \(V_{+1} = D | (MaskSum \& SD) = 0 | (11011011 \& 0) = 0\)
- \(V_0^{\ll} = V_0 \ll 1 = 0\)
- \(V_1^{\ll} = V_1 \ll 1 = 0\)
- \(V_1^{\ll} = V_1^\ll + 1 = 00000001\)
- \(D = M_m \& V_{+1}^\ll = 00100100 \& 00000001 = 0\)
- \(SD = V_{+1}^\ll | (M_m \wedge V_0^\ll) = 00000001 | (00100100 \& 0) = 00000001\)
We see that this gives a different result \(SD = 00000001_2\) instead of \(SD = 00000101_2\).
Looking closer, after step \(7\), \(V_0\) should indicate the cells with vertical difference \(0\) on their right side, ie the first two cells or \(00000011_2\), but instead its value is \(11011011\).
Discussion
I’m not exactly sure what’s wrong, but I think things already fail before the summation, since currently no carry happens at all. A carry is expected because it is the only step that introduces long-range dependencies between bit-positions.
Maybe I have some fundamental misunderstanding of the meaning of the input or output parameters, but the text accompanying the code seems to agree with my understanding. On the other hand, I did not fully understand the brief explanation regarding the runs of ones and how they are resolved by the summation step.
Found the bug
I managed to find the bug with the help of Gary Benson (author of BitPAl). He was so kind to upload his code to github.
- His implementation has an additional ‘fake’ column before column \(0\) without any matches, and which decreases from \(DP[-1][0]=1\) to \(DP[0][0] = 0\).
- An additional carry bit is needed for the addition.
In fact, we don’t need to store the carry explicitly. It turns out the carry is \(1\) exactly when the vertical difference at the start is either \(0\) or \(1\). So the new addition rule is: \[Sum = notM_I + SD + (V_{0,0} | V_{1,0})\]
The corresponding code now takes 20 operations, exactly the same number as Myers’ code. (This is more than the 15 resp. 16 operations that are needed when the pattern is less than 64 characters long, since the carries between adjacent words have quite some overhead.)
pub fn compute_block<P: Profile, H: HEncoding>(h0: &mut H, v: &mut V, ca: &P::A, cb: &P::B) {
let eq = P::eq(ca, cb); // this one is not counted as an operation
let (vm, vmz) = v.m_mz();
let eq = eq | vm;
let ris = !eq;
let notmi = ris | vmz;
// NEW: We add an additional carry when the input difference is 0 or +1.
let carry = h0.z() + h0.p();
let masksum = notmi.wrapping_add(vmz).wrapping_add(carry) & ris;
let hz = masksum ^ notmi ^ vm;
let hp = vm | (masksum & vmz);
let hzw = hz >> (W - 1);
let hpw = hp >> (W - 1);
let hz = (hz << 1) | h0.z();
let hp = (hp << 1) | h0.p();
*h0 = H::from(hzw, hpw);
let vm = eq & hp;
let vmz = hp | (eq & hz);
*v = V::from(vm, vmz);
}
Outlook
I should benchmark the BitPAl code compared to Myers’ bitpacking. But since they use the same number of instructions, I doubt performance will differ much if at all. Maybe one of the two allows for slightly better pipelining though.
More importantly: a lot of instructions (6/20) are spent on carrying bits between words. It should be possible to reduce this. In Figure 1 the vertical delta on the left can take \(3\) possible values and hence requires \(2\) bits to encode. But if we were to take the delta along a diagonal edge as input, there can be only \(2\) possible values and a single bit is sufficient to encode this information. This way it may be possible to process a \(1\times 63\) block using 2 to 4 fewer instructions, which could give up to \(20\%\) speedup.