These are some notes about linear time suffix array (SA) construction algorithms (SACA’s).
- At the bottom you can find a visualization.
- This page has an interactive demo.
History of suffix array construction algorithms:
- 1990 first algorithm: Manber and Myers (1993)
- 2002 small/large suffixes, explained below: Ko and Aluru (2005)
- 2009 recursion only on LMS suffixes: Nong, Zhang, and Chan (2009)
These slides from Stanford are a nice reference for the last algorithm.
Notation
- String \(S = s_0\dots s_{n-1}s_n\).
- $s_n=\$$ is the sentinel, smaller than all other characters.
- Suffix from \(i\): \(S_i := s_i\dots s_n\).
- \(i\) indexes the string \(S\).
- \(j\) indexes the suffix array \(A\).
- Let \(P_i\) be the position of suffix \(S_i\) in the suffix array.
- \(A_{P_i} = i\) and \(P_{A_j}=j\) by definition.
- The previous-suffix and next-suffix of \(S_i\) are \(S_{i-1}\) and \(S_{i+1}\) respectively.
Small and Large suffixes
- Suffix \(S_i\) is small (S-suffix) when \(S_i < S_{i+1}\). \(S_n\) is small by definition.
- Suffix \(S_i\) is large (L-suffix) when \(S_i > S_{i+1}\).
- Equality isn’t possible because of the sentinel.
Then by definition:
- when \(S_i\) is small: \(P_i < P_{i+1}\), ie S-suffixes come before their next-suffix.
- when \(S_i\) is large: \(P_i > P_{i+1}\), ie L-suffixes come after their next-suffix.
Lemma 1: When an S-suffix and L-suffix start with the same character \(c\), the L-suffix comes before the S-suffix in the suffix array.
Proof:
- The S-suffix is of the form $c^x d …$, with \(d>c\) and \(x>0\).
- The L-suffix is of the form $c^y b …$, with \(b<c\) and \(y>0\).
- Since \(b<c<d\), no matter what \(x\) and \(y\) are, the L-suffix is less than the S-suffix.
Building the suffix array from a smaller one
It turns out we can build the SA of \(S\) once we know the SA-order of all small suffixes.
Lemma 2: The set of L-suffixes $\{S_i : s_i =c \text{ and $S_i$ is large }\}$ starting with the same character \(c\) occurs in the same order in the SA as the corresponding next-suffixes \(S_{i+1}\).
Proof: This follows simply from the fact that a set of strings starting with \(c\) can be sorted by only comparing them from the second character onward.
Extension algorithm: This gives the following algorithm to build \(A\) from the partial suffix array of small suffixes:
- Start by initializing a bucket for each character \(c\) in \(S\): Determine the position in \(A\) of the first and last suffix starting with \(c\) by counting the number of characters in \(S\) that are \(<c\) and \(\leq c\) respectively.
- By Lemma 1, the S-suffixes starting with character \(c\) come after the L-suffixes starting with \(c\), and hence can be copied in their already-sorted order to the end of bucket \(c\).
- Now we iterate over the suffix array position \(j\) from \(0\) to \(n\) to fill in the large suffixes in the right places. Recall that \(S_{A_j}\) is the suffix at position \(j\) of the suffix array, and \(S_{A_j-1}\) is its previous-suffix. Also, \(A_0 = n\) by definition, since $S_n = \$$ is minimal.
- If the previous-suffix \(S_{A_j-1}\) is small, it is smaller than \(S_{A_j}\) and hence already positioned at a smaller position \(j’ = P_{A_j-1} < j\).
- If the previous-suffix \(S_{A_j-1}\) is large, this is the next-smallest
suffix starting with character \(c=s_{A_j-1}\). Indeed, by Lemma 2, any smaller
L-suffix starting with \(c\) has a smaller next-suffix, which has been
processed already (seen at position \(< j\)), while any larger L-suffix has a larger next-suffix, which
has not been processed already (not seen at position \(\leq j\)).
Write \(A_j-1\) to the first empty slot in the bucket for \(c\).
Once \(j\) reaches \(n\), this algorithm has completely filled in \(A\). Note that it can never run into empty slots.1
Visualization
I wrote a small visualizer for the algorithm above, see this repo and this post. You can use it to visualize the algorithm for any input string.
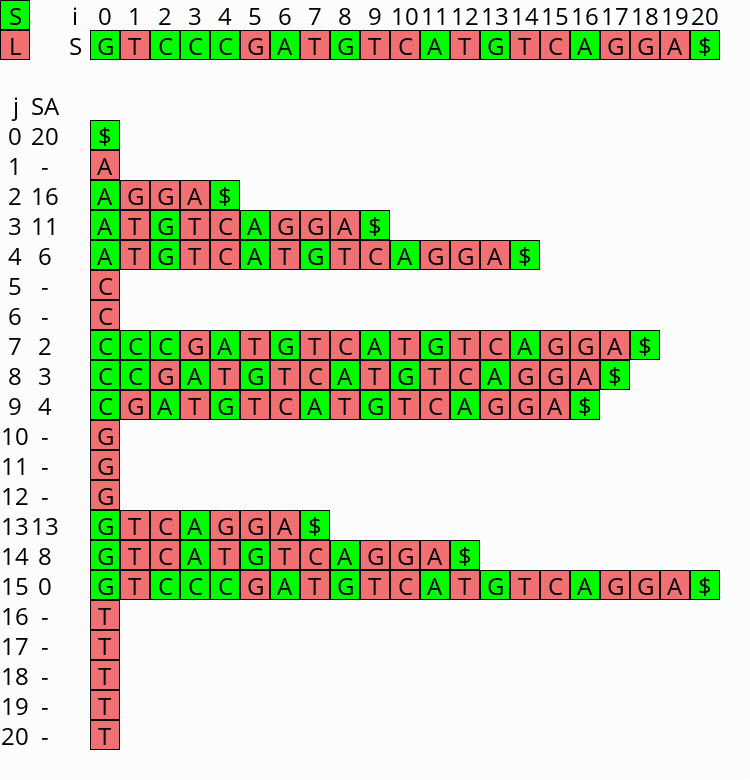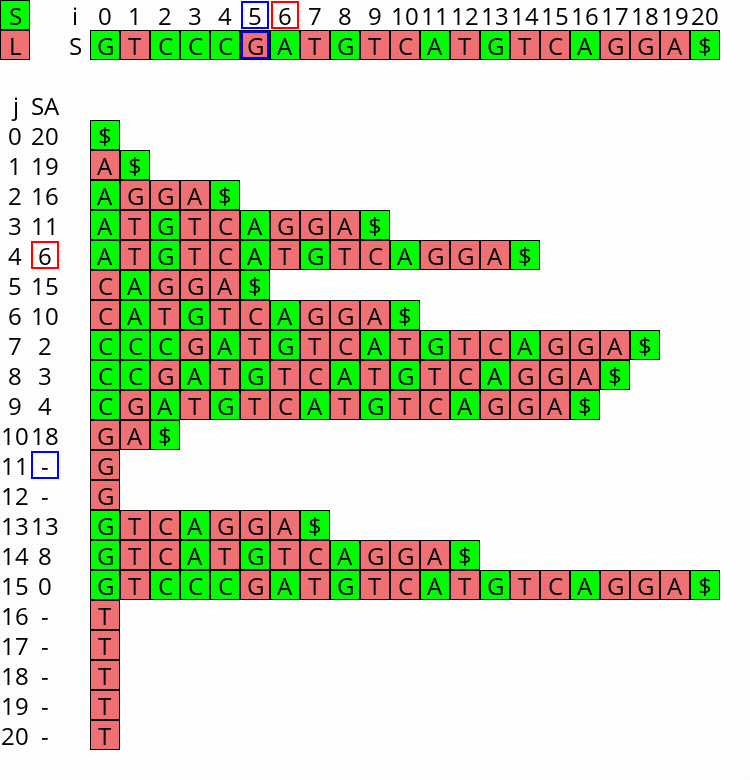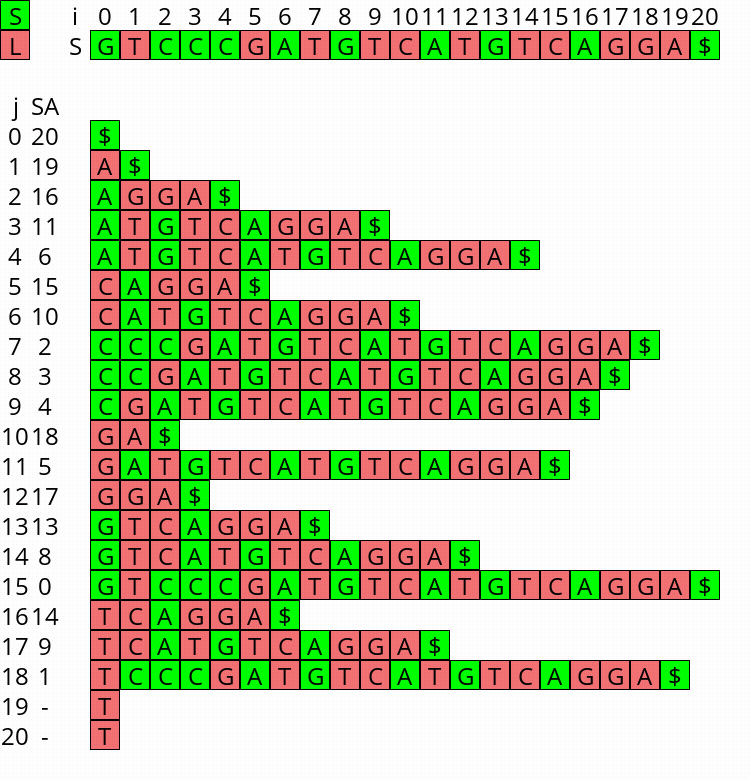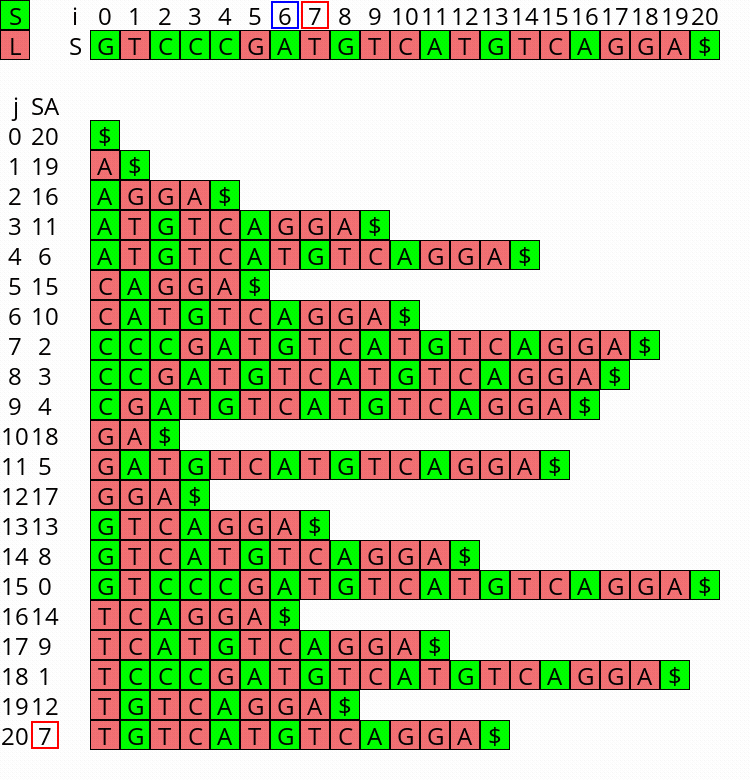
Figure 1: Constructing the complete suffix array starting after step 2 above, with the small suffixes already filled at the ends of their buckets.
References
Proof omitted. ↩︎