These are some (biased) comments on “Greedymini: Generating Low-Density Dna Minimizers”
(Golan et al. 2024), which introduces the GreedyMini minimizer scheme.
(Meanwhile, this has been published as Golan et al. (2025).)
At the bottom, there are also some comment on Golan and Shur (2025).
Overview Link to heading
The GreedyMinimizer is very cute and simple idea, and works as follows:
- Start with the set of all windows of length \(\ell=w+k-1\).
- Pick a k-mer with minimal ratio
\[
\frac{\text{charged occurrences}}{\text{total occurrences}}
\]
where ’total occurrences’ is the number of windows containing the k-mer, and
‘charged occurrences’ (my term) is the number of windows where the k-mer
occurs as a prefix or suffix.
- Intuitively, this makes a lot of sense, since this locally minimizes the fraction of charged windows.
- Remove windows containing the chosen k-mer from the set.
- Repeat until all windows are covered.
Then, some additional techniques are applied:
- Approximation: sampling not the best but a near-best k-mer, to allow for some randomness in the process.
- A greedy local search/hill-climbing, that tries swapping k-mers with adjacent order.
- Extension to larger \(k\) and larger \(\sigma\) by ‘ignoring’ part of the entropy in the k-mer, using a GreedyMini scheme for smaller \(k’\) and \(\sigma’\), and then breaking ties using the ignored entropy.
- Extension to larger \(w>k\), by simply using a smaller \(w\sim k\).
The method can also be applied to obtain sequence specific minimizers.
The results are significantly closer to optimal density minimizer schemes, which is really impressive! I keep thinking that the schemes we have now are the best we’ll ever have, but no, improvements keep coming! At this point, I’m slowly starting to think that (for large alphabets) the lower bound might be completely attainable everywhere.
Also, it is nice to see this scheme ‘confirm’ the lower bound: the density ‘saturates’ as \(k\) grows to \(w\). And then as soon as \(k\geq w+1\), the density drops steeply again, just like the lower bound.
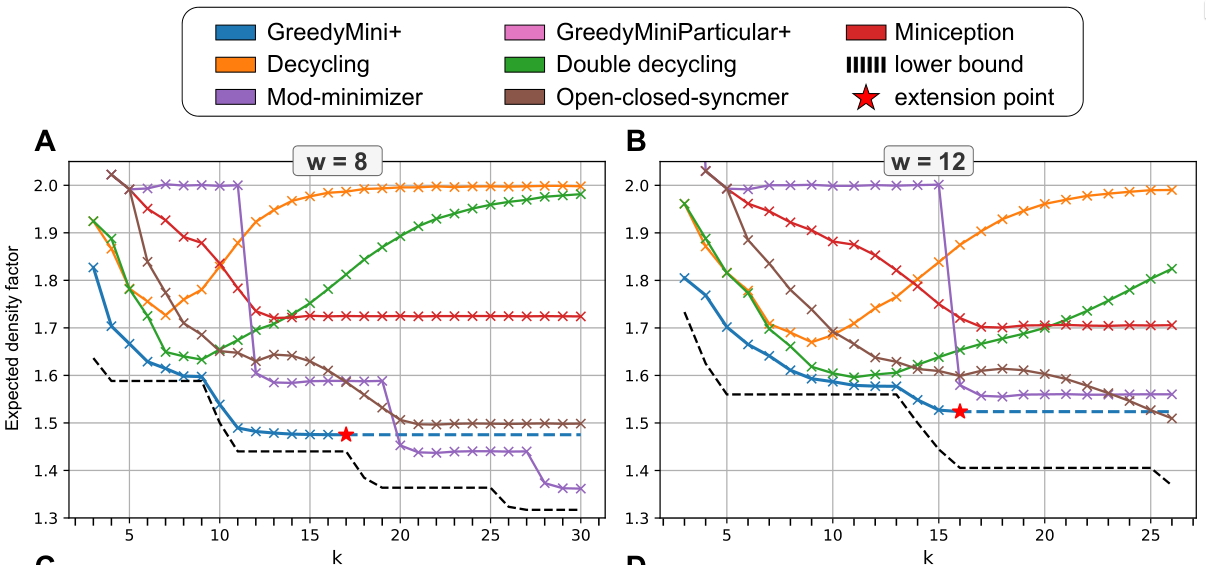
Figure 1: Results of the GreedyMini. As can be seen, the achieve much lower density than other existing schemes. For (k<w/2) they improve a lot over double decycling, and for (kin {w-1, w}), they appear very close to optimal.
My main takeaway from this paper is:
Can we design and understand ‘pure’, memory-free, schemes with a similarly low density?
Detailed comments Link to heading
Terminology Link to heading
A number of terms in the preprint deviate from established terminology (mostly by the papers of Zheng and Marçais):
- Usually
particular densityis used for specific sequences, anddensityis the expected particular density on a random string. Thus, to me,expected densityparses as the expected value of the expected particular density, which is redundant. Prefer justdensity. - In Golan and Shur (2025), gamechanger was introduced instead of the more common charged window. But now it’s charged window again.
- In Golan and Shur (2025), marked positions and markup of \(S\) are introduced, but in the current work those are dropped again.
Abstract Link to heading
(I’m in a pedantic mood — I’m sorry.)
Minimizers is […] . It is […]
Minimizers is plural?
Minimizers that achieve the smallest number of selected k-mers over a random DNA sequence, termed expected density, are desired […].
(expected) densityis not the smallest number of selected k-mers.- ’the number of selected k-mers over a random sequence’ is missing an ’expected’ somewhere.
- (nit) density is not only defined for DNA sequences.
Yet, no method to date exists to generate minimizers that achieve minimum expected density.
What does minimum mean? Some existing scheme is best. Probably you mean
optimal (equal to the lower bound) instead? But then you should qualify it
with for all $k, w, \sigma$ or so, since the mod-minimizer is near-optimal
when e.g.~\(k=w+1\) and \(\sigma\to\infty\).
Moreover, existing selection schemes fail to achieve low density for values of \(k\) and \(w\) that are most practical for high-throughput sequencing algorithms and datastructures.
You seem to focus mostly on \(k \sim w\). In this regime, (double) decycling minimizers, are pretty good? And for \(k>w\), the mod-minimizer is pretty good. (In general, I’d argue all existing schemes are already pretty close to the density lower bound, and hence that they all achieve ’low density’.)
Moreover, we present innovative techniques to transform minimizers […] to larger \(k\) values, […].
This was done before by Marçais, DeBlasio, and Kingsford (2018), called the naive extension (see 3.1.1), and by DeBlasio et al. (2019) (see 3.1).
practical values of \(k\) and \(w\)
Can you be more specific? Since you are hiding exponential running times, what about e.g.~\((k, w) \sim (22, 42)\)?
Generally, it seems this method cannot go much beyond \(k=15\) since it needs \(\sigma^k\) memory?
both expected and particular densities
So far you were using density to mean what previous work calls particular density, but now you also use particular density. Be consistent.
densities much lower compared to existing selection schemes
Please quantify.
We expect
GreedyMini+to improve the performance of many high-throughput sequencing algorithms and data structures
One drawback of GreedyMini seems that it uses memory exponential in \(k\). For
\(k>21\) or so, the order will likely not fit in cache, and each processed k-mer
requires a read from main memory. Even in the best case, this will limit
(single threaded) throughput to around \(10ns\) per kmer, over \(10\times\) slower
than my fast minimizer implementation.
Preliminaries Link to heading
- \(d_L\) missing mathcal
- \(\mathcal L\) is weird for a single scheme; in Groot Koerkamp and Pibiri (2024) that’s the set of all local schemes instead.
- \([a, b)\) is usually the half-open interval of real numbers, not the set of
integer \(\{a, \dots, b-1\}\). Use \([b]\) instead?
- You define \([B]\) as the indicator function of a boolean expression currently, but I’m not sure if that’s actually used.
- You may want to define a UHS order to have a
rankthat takes \(O(1)\) time to evaluate. - I believe existing literature consistently uses windows of length \(\ell =
w+k-1\) and (charged) contexts of length \(w+k\). Thus, a charged window is confusing.
- If you do keep windows, it should consistently be $(w+k)$-window instead of just window.
Methods Link to heading
Theorem 1:
- I think this assumes that
rankis \(O(1)\). - I don’t think the tree-based proof is needed. Instead, one can just evaluate the particular density on an order-\((k+w)\) De Bruijn sequence (Marçais et al. 2017 Lemma 4) using an amortized \(O(1)\) algorithm.
- I think this assumes that
Theorem 2: This doesn’t seem to be used anywhere. The result seems a bit niche.
GreedyMini: Can you say something about how the score function ends up trying to space sampled k-mers exactly \(w\) positions apart on the De Bruijn graph.
It would be interesting to do some statistics/analysis on this.
How do you count when a k-mer occurs multiple times in a window?
When talking about running times of
GreedyMini, consider being more explicit on whether this is the construction of the minimizer, or the evaluation. Specifically for the sequence-specific scheme, this is easily confused.For the local search, would it make sense to instead of a full order on k-mer, consider instead a poset (partially ordered set), where k-mers that cannot occur together in a window (because \(k>w\)) are incomparable. Then, instead of swapping any adjacently-ranked k-mers, one can consider only swapping k-mers where this actually has an effect on the sampled k-mers.
Algorithm 1: swap lines 7 and 8?
3.5 Transformations Link to heading
Both Theorem 5 and Theorem 6 seem overly complex.
On a high level, given a scheme on $k$-mers over \(\sigma\), extending that to a scheme over $k’$-mers over \(\sigma’\) with \(k’\geq k\) and \(\sigma’\geq \sigma\) never hurts. Each $k’$-mer just has more bits of information available, and ignoring most of that is never worse than the underlying \((k, \sigma)\) scheme.
- Let \(\tau_0\) be the ’null-order’ on \(\Gamma^k\) that maps everything to \(0\). Then it trivially holds that \(d_{(\rho\times \tau_0, w)} = d_{(\rho, w)}\).
- Adding tiebreaking by using \(\tau\) instead of \(\tau_0\) can only decrease density.
- Thus, \(d_{(\rho\times \tau, w)} \leq d_{(\rho\times \tau_0, w)} = d_{(\rho, w)}\), and there is no need for the ‘minimum of two values is less than the average’ part of the theorem.
- Similarly, the order \(\rho’\) on $(k+1)$-mers that ignores the last character
has density \(d_{(\rho’, w)} = d_{(\rho, w)}\), and any kind of tie-breaking will only
decrease this: \(d_{(\rho_1, w)} \leq d_{(\rho’, w)} = d_{(\rho, w)}\)
- (Side note: maybe also add \(k\) to the subscript for clarity?)
- This is also the ’naive extension’ of Marçais, DeBlasio, and Kingsford (2018 Lemma 4) and DeBlasio et al. (2019).
- The cited Zheng, Kingsford, and Marçais (2021a 2.1.3) only states the fact for local schemes, but also makes it clear that the same positions are sampled, and thus that if the initial scheme is a minimizer scheme, the extended scheme is one as well.
- How does the performance of GreedyMini change if instead of the best of the two versions, just the forward one is taken? (For both theorems.) You mentioned that typically they perform very similar.
Results Link to heading
- For how long did GreedyMini run?
- The open-closed syncmers in the plots are not published anywhere yet. We just uploaded the open-closed mod-minimizer PDF this weekend :) Should be on bioRxiv soon. Probably best to replace ‘open-closed-syncmer’ with the full ‘OC-mod-mini’ version.
- Cite and compare to DOCKS? That’s a similar method for brute-force construction of UHSes.
- ‘forward local schemes’: just ‘forward schemes’
- For particular schemes, how does this compare to simply sampling every \(w\)’th k-mer from the input sequence?
- For the particular schemes: Have you reached out to the authors?
- Could you provide some intuition why GreedyMini works particularly well for \(w=k\) and \(w=k-1\)?
- Please provide a small table comparing densities of GreedyMini with existing schemes and/or the lower bound, and the percentual improvement, for some \((k,w)\) of your choice.
- Optimal \((k,w)\):
- They are not sorted consistently.
- (They are a subset of cases for which the ILP of Kille et al. (2024 Table 2) finds optimal solutions.)
- ‘requiring more runs with smaller \(\alpha\)’: quantify how much more/how much longer. It’s not clear currently how good GreedyMini is in practice at finding such schemes.
- Fig 3: I don’t think this adds much over Fig 2 A-D, in part because it’s hard to show both the density of GreedyMini and the lower bound.
- A comparison between
GreedyMiniandGreedyMini+(with local search) would be nice. - Some plots showing for some specific \((k,w)\) how the density of
GreedyMini+improves with time/iterations during the local search would be interesting to get an idea of how close to optimal the returned densities are. - How much density is ’lost’ by lifting from \(\sigma=2\) to \(\sigma=4\)? Could you run experiments for small \(k\) and \(w\) and compare results?
- Similarly, how must density is lost by lifting from \(k\) to \(k’>k\)?
- Is it feasible to run some experiments for \(\sigma=256\) or so?
Discussion Link to heading
- ‘This is an acceptable runtime for a wide range of practical values of \(k\) and \(w\).’: Please quantify. There are definitely parameters used in practice that fall outside of what GreedyMini can do.
- Even when the lookup table fits in cache, I suspect that the lookup rate may be a bottleneck in practice.
Comments on “Expected density of random minimizers” Link to heading
- Lemma 1 was done before:
- Proof of Theorem 3 in (Marçais et al. 2017)
- Lemma 4 in (Zheng, Kingsford, and Marçais 2021b)
- Theorem 1: This follows directly from computing the particular density on an order \((w+k)\) De Bruijn sequence.