28000x speedup with Numba.CUDA

24 May 2021 38-minute read

This post is a write-up of how Numba and Numba.CUDA managed to speed up my Python algorithm 28 000 times. First I’ll give some links to useful resources on writing code for CUDA and profiling it. Then I’ll walk you through the changes that sped up my code and show how to use the information available in the profiler.

At the very bottom is a table summarizing all the gains.

Overall, writing CUDA code with Numba.CUDA is very enjoyable and seems to be very similar to writing the equivalent C code. To me, the main drawback is that it is not exactly the same as the C API, which introduces some quirks: one has to be aware of things like cuda.defer_cleanup(), and passing in a list of arrays doesn’t just work. When writing C, it’s very natural to think about the types in an array from the start, while in Python, this may be more of an afterthought and can be more tricky to get right. Lastly, profiling Python code in nvvp doesn’t seem to work, so I had to use nvprof directly instead.

Nevertheless, once you are aware of these issues, writing kernels in Python is very convenient and offers great development speed.

CUDA Overview

In case you’re not yet familiar with CUDA and would like to read up on it, the following resources were very helpful for me. Otherwise, please skip to Optimizing Tensor Sketch below.

CUDA programming guide: It’s a long read, but a good starting point. (Definitely skip sections you don’t find interesting.) Some highlights:
- SIMT architecture
- Throughput per operation per SM
- Shared memory banks
  - Note: the 64-bit mode only existed for CC 3.x.
CUDA best practices guide: Very useful extra information that’s slightly less formal than the programming guide above.
Wikipedia page on CUDA: Compute Capability (aka CC) and architecture per device.
- Note: Compute Capabilities and CUDA SDK versions are not the same.
Hardware specs for different Compute Capabilities
Numba.cuda docs, for writing CUDA kernels in Python.
- Numba gitter, in case you have Numba questions.

And here is also a list of some more blogposts and links, mostly from Nvidia. Note that these are mostly about C/C++, but the Numba.cuda API exactly mirrors the C/C++ CUDA API.

Even easier introduction to CUDA
- All the posts linked at the bottom of that page are also great.
CUDA Memory Model
Volta architecture
Shared Memory
Streams: Running kernels and memory transfers in parallel.
How to overlap Data Transfers
Cooperative Groups: Syncing between groups of threads smaller or larger than a block.
2h talk on optimization
Cache/shared memory trade-off is supported on some devices.
- The Numba API doesn’t expose this, but a workaround is in this issue.

Here’s a quick summary:

The CPU is also called the host.
The GPU is also called the device.
A GPU has multiple independent Streaming Multiprocessors (SMs).
Each SM has its own shared memory used by blocks running on this SM.
The threads in a block are divided in warps consisting of 32 threads.
The threads in a warp all execute synchronously.
The blocks in a kernel/grid can be distributed over multiple SMs.
Each SM can run a number of blocks in parallel, and each block runs on one SM.
The number of warps and blocks a SM can run is bounded by the number of registers each thread uses and the amount of shared memory each block uses.
Kernels can be executed in parallel by assigning them to different non default streams.
Each block has a 1D, 2D, or 3D id/position in the grid.
Each thread has a 1D, 2D, or 3D id/position in its block.
Threads in a kernel can process different parts of the input by using their block and/or thread id as an index into the input data.

Profiling

Profiling is a great way to find the bottlenecks in your CUDA kernels. This section lists the most important tools and commands.

nvprof (docs): The main command line tool for profiling. More on it below.
- Nvidia blogpost
nvvp (docs) is the Nvidia Visual Profiler. It can either display profiles generated by nvprof, or directly profile applications by creating a new session.
- Note: For me, profiling Numba.cuda applications using nvvp sessions didn’t work well. Just running the nvprof command line and importing the result works much more reliably.
Nsight Systems is the successor of nvvp and only works on Pascal or newer architectures (CC 6.0 and higher).
- Nsight Compute: Used to profile single CUDA kernels. You can click on a kernel in the timeline in Nsight Systems and it will open Compute automatically. Sadly my older card isn’t supported so I haven’t used this.
- Nsight Graphics: Similar to Nsight Compute, but for profiling graphics applications instead of CUDA kernels.

The most important invocation of nvprof for me is

nvprof -f -o profile.nvvp ./test.py

which writes a simple timeline of which kernels were launched to profile.nvvp (overwriting existing files with -f). This mode isn’t much slower than the original code. profile.nvvp can be opened in nvvp.

To get detailed statistics on a single kernel, use

nvprof --analysis-metrics -f -o profile.nvvp ./test.py

This is much slower since it reruns the kernel many times, collecting different metrics on each run. You may want to add --profile-from-start off to disable profiling from the start, and call cuda.profile_start() and cuda.profile_stop() in the python code to only profile a part of the code and prevent unneeded detailed analysis of all kernels.

Add the -a instruction_execution flag, in combination with @cuda.jit(debug=True) to see how often instructions are executed inside nvvp.

To get a quick measure of register and memory usage per kernel, run

nvprof --print-gpu-trace ./test.py

The --analysis-metrics mode may give the following error, which requires root to fix: > =78640= Warning: ERR_NVGPUCTRPERM - The user does not have permission to profile on the target device. See the following link for instructions to enable permissions and get more information: https://developer.nvidia.com/ERR_NVGPUCTRPERM

Optimizing Tensor Sketch

In the remainder of this post, I’m working on the algorithm presented in Fast Alignment-Free Similarity Estimation by Tensor Sketching by Amir Joudaki et al. This algorithm is used to quickly ‘sketch’ (i.e. hash into Euclidean space) genomic sequences in order to estimate their similarity.

The algorithm is best described as a DP (Dynamic Programming) over the characters of the sequence. I won’t go into detail here on what the code does; you can have a look at the paper if you’re interested in details.

For speed of iteration and experimentation, I rewrote the algorithm from C++ to Python some time ago, so now the goal is to first make the Python as fast as the C++, and then make it even faster!

To test the speed-ups, I’m running this sketch algorithm on all 1410 sequences in a single 100MB Fasta file containing parts of a human genome.

Note that these speed-ups depend a lot on the specific context, so don’t read too much into the exact numbers.

CPU code

Before moving to GPU code, let’s first have a look at the original Python code and the speed-up from Numba just in time compilation.

V0: Original python code

We start with the piece of code shown below. The sketch method will be called once for each sequence and keeps track of the DP table T. The constructor initializes the hashes and signs arrays, since these are constant between the many calls to sketch.

This code is already using NumPy for the np.roll in the inner loop, which in this case just rotates a one dimensional array over the specified number of positions. It runs in an estimated 7000s or almost 2 hours.

V0: 7000s (Click to toggle)

A = 4
t = 4
D = 96

class TS:
    def __init__(self):
        random.seed(31415)
        # An A*t array of random integers in [0, D)
        self.hashes = np.empty((A, t), dtype=np.int64)
        # An A*t array of random +-1
        self.signs  = np.empty((A, t), dtype=np.int64)
        for c in range(A):
            for k in range(t):
                self.hashes[c][k] = random.randrange(0, D)
                self.signs[c][k] = random.randrange(-1, 2, 2)

    def sketch(self, seq):
        T = np.zeros((t+1, D), dtype=np.int64)
        T[0][0] = 1

        for c in seq:
            for k in range(t-1, -1, -1):
                h = self.hashes[c][k]
                s = self.signs[c][k]
                T[k+1] += s * np.roll(T[k], h)

        return T[t]

V1: Numba

Using Numba’s new @jitclass decorator, we can just-in-time compile the entire TS class. (In contrast, free functions are optimized with @jit or @njit.) This makes the code run in 50s, which should be roughly the same as equivalent C++ code, and is a 140x speed-up from the vanilla Python code!

Numba can not compile all python code, so we have to first allocate the memory for the hashes and signs arrays and only then fill it – wrapping a list comprehension in np.array doesn’t work.

Note that I unrolled the np.roll since it appears that Numba is better at optimizing the manual for loop.

V1: 50s (Click to toggle, changed lines are marked with a +)

 A = 4
 t = 4
 D = 96

+@jitclass([('hashes', nb.int64[:,:]), ('signs', nb.int64[:,:])])
 class TS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int64)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.int64)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

     def sketch(self, seq):
         T = np.zeros((t+1, D), dtype=np.int64)
         T[0][0] = 1

         for c in seq:
             for k in range(t-1, -1, -1):
                 h = self.hashes[c][k]
                 s = self.signs[c][k]
+                for l in range(D):
+                    r = l+h if l+h < D else l+h-D
+                    T[k+1][l] += s * T[k][r]

         return T[t]

V2: Multithreading

The code is already fairly simple and optimized, so there’s not much more we can do. To extract the last bit of performance, we can use the multiprocessing library to run it on all 8 threads of my laptop simultaneously. That brings the runtime down to 12s, a nice 4x improvement.

GPU code

Now it’s time to move to writing GPU code. The times reported below are all using a GTX 960M with compute capability 5.0, having 5 SMs and 65KB shared memory per SM.

V3: A first GPU version

Looking at the code for V1 above, notice that the t*D iterations over k and l are almost independent of each other. The only conflict is that we write to T[k+1][l], which may simultaneously be read as T[k2][l2+h] for some other k2 and l2. This can be fixed though, by first storing the result in a temporary array and only then copying it back into the original T array.

Thus, we can use a single block of t*D threads to process a sequence, where each thread is identified by a fixed k and l. Each thread loops over all characters in the sequence, sums two array elements from Tin, and writes them to Tout. Then we synchronize all threads and copy the result from Tout back to Tin, so that the data is ready for the next iteration.

Note that Tin and Tout are stored in shared memory so that reading and writing these is fast, and the data is shared between all threads processing the current sequence.

The sketch function launches one kernel to sketch the current sequence, and the kernel has one block (the (1,1) parameter) and t*D threads (the (self.t, self.D) parameter). The output array T is created outside the kernel and results will be written to it by the kernel.

It turns out that this code takes 100s to process all sequences – much slower than our single threaded python before…

V3: 100s (Click to toggle)

A = 4
t = 4
tp1 = t+1
D = 96

@cuda.jit
def gpu_sketch(hashes, signs, seq, T):
    k = cuda.threadIdx.x
    l = cuda.threadIdx.y
    assert k < t
    assert l < D

    # Shared memory for temporary DP tables.
    Tin = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)
    Tout = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)

    Tin[k][l] = 0
    Tin[k+1][l] = 0
    Tout[k][l] = 0
    Tout[k+1][l] = 0

    cuda.syncthreads()

    Tin[0][0] = 1
    Tout[0][0] = 1

    cuda.syncthreads()

    # Loop over characters in the sequence.
    for c in seq:
        h = hashes[c][k]
        s = signs[c][k]
        # Compute the shifted target index, avoiding a modulo operation.
        r = l + h
        r -= D if r >= D else 0
        # Write to output tensor.
        Tout[k+1][l] = Tin[k+1][l] + s * Tin[k][r]
        cuda.syncthreads()
        # Copy output back to input.
        Tin[k+1][l] = Tout[k+1][l]
        cuda.syncthreads()

    # Copy to result.
    T[k+1][l] = Tout[k+1][l]


class GTS:
    def __init__(self):
        random.seed(31415)
        # An A*t array of random integers in [0, D)
        self.hashes = np.empty((A, t), dtype=np.int64)
        # An A*t array of random +-1
        self.signs  = np.empty((A, t), dtype=np.int64)
        for c in range(A):
            for k in range(t):
                self.hashes[c][k] = random.randrange(0, D)
                self.signs[c][k] = random.randrange(-1, 2, 2)

    def sketch(self, seq):
        # Allocate memory for the response.
        T = np.zeros((t+1, D), dtype=np.float32)
        # One thread per (k, l) <= (t, D)
        gpu_sketch[(1,1), (t, D)](self.hashes, self.signs, seq, T)
        return T

V4: Parallel kernel invocations

Each of our kernels only consists of 1 block currently, and since we run them all in sequence, this only runs on 1 SM at a time. To keep the multiple SMs busy, we can start multiple kernels in parallel. This is done using streams. When we pass a stream argument to a kernel or a memory copy, that operation will happen asynchronously of the CPU code, but in sequence with all the other operations on the same stream.

Thus, we manually copy each kernel parameter to the device using cuda.to_device. (See the code below for details.) In order for the sketch function to be completely asynchronously, we can’t do the device to host copy inside it, since that must wait for the kernel to complete. Instead, we just return the device array d_T, so that we can copy all the results back to the host after all the sketching is done.

Some notes: - We could use multiprocessing to launch multiple kernels in parallel, but this has some issues. multiprocessing.dummy (which is a wrapper around threading) could also be used, but in the end it’s much cleaner to write the code in such a way that all the kernel invocations run asynchronously of the Python code, so that the Python code itself can remain simple and single threaded. - Unlike in the C++ API, the kernel launch takes the stream as 3rd argument instead of 4th argument. - T is directly allocated on the device using cuda.device_array. - Since the self.hashes and self.signs parameters are the same for each invocation of sketch, it’s nicer to copy them only once in the constructor so we can reuse them from the device memory on further invocations.

This brings the running time down to 58s. Since my GPU has 5 SMs, and we got 100s using only a single SM, something must be up with how efficient this parallelization is.

So, let’s run the profiler on our code to see a timeline of all kernels invocations:

nvprof -f -o profile.nvvp ./test.py && nvvp ./profile.nvvp

zoomed in:

It seems that the kernels aren’t actually running in parallel! Or rather, they do, but somehow there is some unnecessary syncing going on, meaning the CPU code (Python application) is waiting for all kernels to finish before starting new kernels.

It turns out the Python garbage collector is responsible for this: we create a device array d_seq that goes out of scope at the end of sketch. After we have launched a few kernels, the garbage collector kicks in and wants to deallocate these device arrays. But to do that, Numba will synchronize and wait for all kernels to be finished. The fix turns out to be simple: we can wrap the testing code in

with cuda.defer_cleanup():

which postpones all deallocation of device arrays to when the context is over.

At first I fixed this by returning a tuple (d_seq, d_T) from the sketch function, so that neither device array goes out of scope. But the defer_cleanup() solution is much cleaner.

Running the profiler again, we now get showing 16 kernels running in parallel during the entire program.

This reduces the runtime to 13s, 8 times faster than the synchronous version! (Note that while we are now running 16 kernels, there are still only 5 SMs, so we can not just expect a 16x speed-up.) Surprisingly, that’s still only on par with the multithreaded CPU code.

My CC 5.0 GPU (GTX 960M) supposedly can run 32 kernels in parallel but in my runs it’s always capped at 16. I have no idea why it doesn’t go higher.

V4: 13s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96

 @cuda.jit
 def gpu_sketch(hashes, signs, seq, T):
     k = cuda.threadIdx.x
     l = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)
     Tout = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)

     Tin[k][l] = 0
     Tin[k+1][l] = 0
     Tout[k][l] = 0
     Tout[k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0] = 1
     Tout[0][0] = 1

     cuda.syncthreads()

     # Loop over characters in the sequence.
     for c in seq:
         h = hashes[c][k]
         s = signs[c][k]
         # Compute the shifted target index, avoiding a modulo operation.
         r = l + h
         r -= D if r >= D else 0
         # Write to output tensor.
         Tout[k+1][l] = Tin[k+1][l] + s * Tin[k][r]
         cuda.syncthreads()
         # Copy output back to input.
         Tin[k+1][l] = Tout[k+1][l]
         cuda.syncthreads()

     # Copy to result.
     T[k+1][l] = Tout[k+1][l]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int64)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.int64)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

+        self.d_hashes = cuda.to_device(self.hashes)
+        self.d_signs = cuda.to_device(self.signs)
+
     def sketch(self, seq):
         # Allocate memory for the response.
+        stream = cuda.stream()
+        d_seq = cuda.to_device(seq, stream=stream)
+        # Allocate T on the device directly.
+        d_T = cuda.device_array((t+1, D), dtype=np.float32, stream=stream)
+
         # One thread per (k, l) <= (t, D)
+        gpu_sketch[(1,1), (t, D), stream](self.d_hashes, self.d_signs, d_seq, d_T)
+
+        return d_T
+

V5: Single kernel with many blocks

Instead of launching one kernel per sequence, it’s better to launch a single kernel for all sequences, containing one block per sequence. This reduces the overhead of launching kernels and gives a bit more freedom to the block scheduler.

To do this, we concatenate all sequences into a single long sequence, and pass the start and end index of each sequence to each block.

This reduces the runtime to 11.0s.

Note that processing any number of sequences of at least 2 in a single kernel gets this runtime of 11.0s, (probably because 2*16=32 blocks is enough to saturate all SMs,) but having all sequences in one kernel is the most convenient.

V5: 11s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96

 @cuda.jit
+def gpu_sketch(hashes, signs, seq, starts, T):
+    seqid = cuda.blockIdx.x
+    start = starts[seqid]
+    end = starts[seqid+1]
+
     k = cuda.threadIdx.x
     l = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)
     Tout = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)

     Tin[k][l] = 0
     Tin[k+1][l] = 0
     Tout[k][l] = 0
     Tout[k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0] = 1
     Tout[0][0] = 1

     cuda.syncthreads()

     # Loop over characters in the sequence.
+    for i in range(start, end):
+        c = seq[i]
         h = hashes[c][k]
         s = signs[c][k]
         # Compute the shifted target index, avoiding a modulo operation.
         r = l + h
         r -= D if r >= D else 0
         # Write to output tensor.
         Tout[k+1][l] = Tin[k+1][l] + s * Tin[k][r]
         cuda.syncthreads()
         # Copy output back to input.
         Tin[k+1][l] = Tout[k+1][l]
         cuda.syncthreads()

     # Copy to result.
+    T[seqid][k+1][l] = Tout[k+1][l]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int64)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.int64)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

+    def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()
+
+        blocks = len(seqs)
+
+        seq = np.concatenate(seqs)
+        starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)
+
         d_seq = cuda.to_device(seq, stream=stream)
+        d_starts = cuda.to_device(starts, stream=stream)
+        d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (k, l) <= (t, D)
+        gpu_sketch[(blocks,1), (t, D), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V6: Detailed profiling: Kernel Compute

Running nvprof with --analysis-metrics shows the following plot under Kernel Compute in the unguided analysis section: 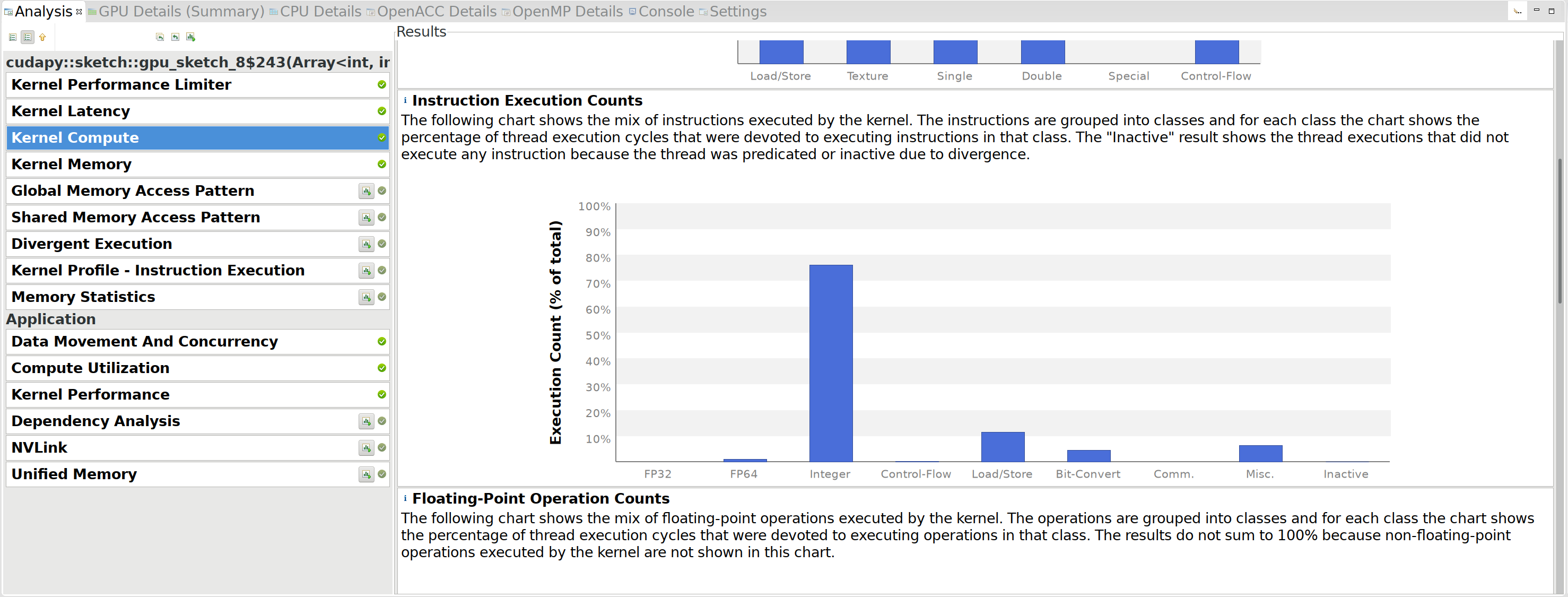Apparently, we are doing some 64-bit floating point operations (FP64 in the 2nd column). This is bad, because according to the throughput table a compute capability 5.0 SM can only do 4 64-bit floating point operations per clock cycle, compared to 128 32-bit floating point operations. So let’s find out where those operations happen and get rid of them.

After some searching, it turns out that self.hashes and self.signs were both stored and passed as arrays of np.int64. Because of that, the s * Tin[k][r] operation was casting Tin[k][r] from a float32 to a float64 and doing a 64-bit multiplication. Changing signs to np.float32 and hashes to np.int32 removed all the 64-bit floating point operations: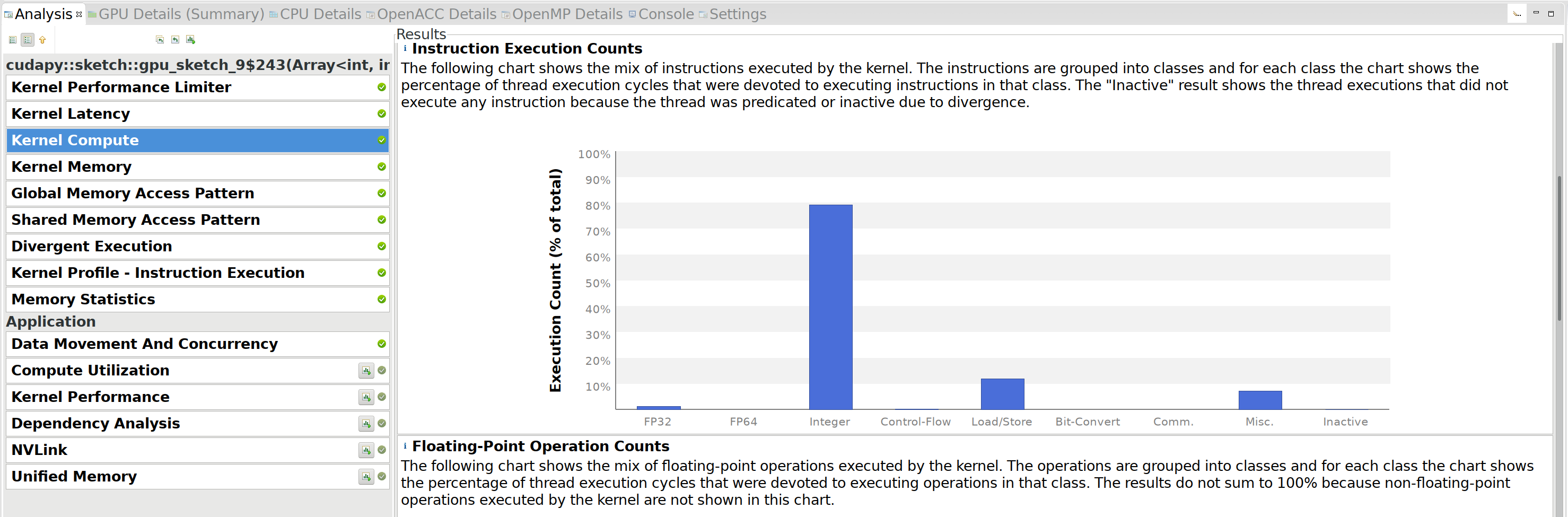

In the process, I have also added the fastmath=True option to the @cuda.jit decorator, to potentially speed up floating point operations by allowing slightly less precise results. (Although it seems this only really matters for division and exponentiation operations, which we’re not doing here.)

This gives a factor 2 speedup to 5.5s!

V6: 5.5s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96

+@cuda.jit(fastmath=True)
 def gpu_sketch(hashes, signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

     k = cuda.threadIdx.x
     l = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)
     Tout = cuda.shared.array(shape=(tp1, D), dtype=nb.float32)

     Tin[k][l] = 0
     Tin[k+1][l] = 0
     Tout[k][l] = 0
     Tout[k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0] = 1
     Tout[0][0] = 1

     cuda.syncthreads()

     # Loop over characters in the sequence.
     for i in range(start, end):
         c = seq[i]
         h = hashes[c][k]
         s = signs[c][k]
         # Compute the shifted target index, avoiding a modulo operation.
         r = l + h
         r -= D if r >= D else 0
         # Write to output tensor.
         Tout[k+1][l] = Tin[k+1][l] + s * Tin[k][r]
         cuda.syncthreads()
         # Copy output back to input.
         Tin[k+1][l] = Tout[k+1][l]
         cuda.syncthreads()

     # Copy to result.
     T[seqid][k+1][l] = Tout[k+1][l]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
+        self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
+        self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (k, l) <= (t, D)
         gpu_sketch[(blocks,1), (t, D), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V7: Detailed profiling: Kernel Latency

Looking further, we see that synchronization is one of the main stall reasons: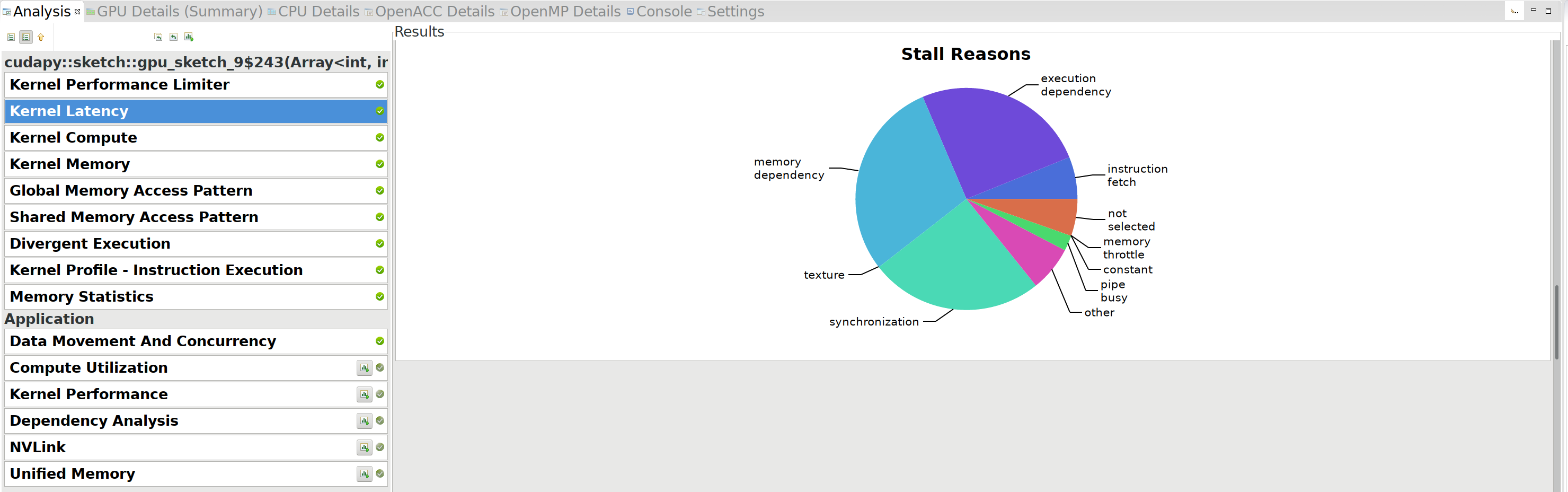

Currently, we do two syncs for each character: one after computing the new value, and one after copying that value back to the original array. It turns out we can do better by omitting that copy, and instead just reading from Tout on the next iteration. To simplify the implementation, we merge Tin and Tout to a single 3D array with 2 layers, using a new index j to indicate which layer we are currently reading from.

This again shaves off almost a second, going to 4.7s.

V7: 4.7s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96

 @cuda.jit(fastmath=True)
 def gpu_sketch(hashes, signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

     k = cuda.threadIdx.x
     l = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
+    Tin = cuda.shared.array(shape=(2, tp1, D), dtype=nb.float32)

+    Tin[0][k][l] = 0
+    Tin[0][k+1][l] = 0
+    Tin[1][k][l] = 0
+    Tin[1][k+1][l] = 0

     cuda.syncthreads()

+    Tin[0][0][0] = 1
+    Tin[1][0][0] = 1

     cuda.syncthreads()

+    j = 0
+
     # Loop over characters in the sequence.
     for i in range(start, end):
         c = seq[i]
         h = hashes[c][k]
         s = signs[c][k]
         # Compute the shifted target index, avoiding a modulo operation.
         r = l + h
         r -= D if r >= D else 0
         # Write to output tensor.
+        Tin[1-j][k+1][l] = Tin[j][k+1][l] + s * Tin[j][k][r]
+        j = 1-j
         cuda.syncthreads()

     # Copy to result.
+    T[seqid][k+1][l] = Tin[j][k+1][l]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (k, l) <= (t, D)
         gpu_sketch[(blocks,1), (t, D), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V8: Detailed profiling: Shared Memory Access Pattern

Under the Shared Memory Access Pattern tab, we can find the following: 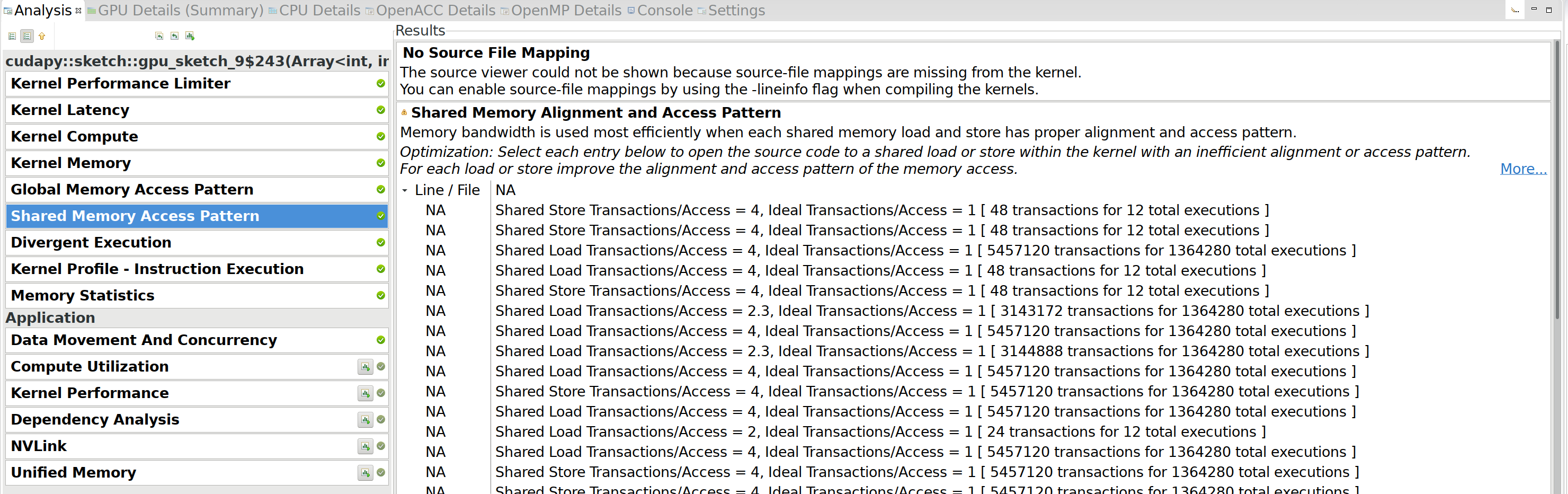These issues are because shared memory uses banks, and code is more efficient if the 32 threads in a warp do not access multiple addresses within a single bank during a single instruction.

On close inspection of the code, it turns out that k = cuda.threadIdx.x is the ‘fast’ index, and l = cuda.threadIdx.y is the ‘slow’ index. Since threads are grouped into warps by their linear index, they first form groups with the same l.

The memory accesses Tin[j][k+1][l] will be more efficient when l is the fast index instead, so that consecutive threads read consecutive memory addresses. This is an easy fix, since we can just swap the block dimensions when launching the kernel, that brings the runtime down to 4.6s. (Not much, but at least we fixed those warnings.)

V8: 4.6s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96

 @cuda.jit(fastmath=True)
 def gpu_sketch(hashes, signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

+    l = cuda.threadIdx.x
+    k = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(2, tp1, D), dtype=nb.float32)

     Tin[0][k][l] = 0
     Tin[0][k+1][l] = 0
     Tin[1][k][l] = 0
     Tin[1][k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0][0] = 1
     Tin[1][0][0] = 1

     cuda.syncthreads()

     j = 0

     # Loop over characters in the sequence.
     for i in range(start, end):
         c = seq[i]
         h = hashes[c][k]
         s = signs[c][k]
         # Compute the shifted target index, avoiding a modulo operation.
         r = l + h
         r -= D if r >= D else 0
         # Write to output tensor.
         Tin[1-j][k+1][l] = Tin[j][k+1][l] + s * Tin[j][k][r]
         j = 1-j
         cuda.syncthreads()

     # Copy to result.
     T[seqid][k+1][l] = Tin[j][k+1][l]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

+        # One thread per (l, k) <= (D, t)
+        gpu_sketch[(blocks,1), (D, t), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V9: More work per thread

Looking back at the 2nd figure of V6, we notice that we actually do very few floating point operations compared to integer operations. To improve this, we can try to do more than one ‘unit’ of work per kernel. Instead of assigning a single l to each kernel, we can instead try to assign each kernel L different values of l, and launch t*(D/L) threads instead of t*D. (Note: Multiple values of k won’t work because those have a different sign[c][k] and hash[c][k].) These values can be either consecutive ([0..L)) or strided ({0, D/L, 2D/L, ...}). From a shared memory access point of view, strided should be faster, but in practice, consecutive turned out to be better in this case. (I don’t know why.)

After some testing, the optimal value of L is 6. This makes some sense, because 96/6 = 16, so each warp corresponds to exactly two layers of the DP.

The number of shared memory reads per floating point operation will also go down now, because we reuse the reads of h = hashes[c][k] and s = signs[c][k] across multiple values of l.

This given an almost 3x improvement, and the runtime is now 1.88s.

V9: 1.88s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96
+L = 6
+assert D%L == 0
+DL = D//L
+threads = t*DL

 @cuda.jit(fastmath=True)
 def gpu_sketch(hashes, signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

     l = cuda.threadIdx.x
     k = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(2, tp1, D), dtype=nb.float32)

     Tin[0][k][l] = 0
     Tin[0][k+1][l] = 0
     Tin[1][k][l] = 0
     Tin[1][k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0][0] = 1
     Tin[1][0][0] = 1

     cuda.syncthreads()

     j = 0

     # Loop over characters in the sequence.
     for i in range(start, end):
         c = seq[i]
         h = hashes[c][k]
         s = signs[c][k]
         # Compute the shifted target index, avoiding a modulo operation.
+        for ll in range(L*l, L*(l+1)):
+            r = ll + h
+            r -= D if r >= D else 0
+            # Write to output tensor.
+            Tin[1-j][k+1][ll] = Tin[j][k+1][ll] + s * Tin[j][k][r]
         j = 1-j
         cuda.syncthreads()

     # Copy to result.
+    for ll in range(L*l, L*(l+1)):
+        T[seqid][k+1][ll] = Tin[j][k+1][ll]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (l, k) <= (D, t)
+        gpu_sketch[(blocks,1), (DL, t), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V10: Cache seq to shared memory

Instead of reading the characters in seq from global memory at each iteration, we can read a segment of characters at a time and explicitly cache them in shared memory. This won’t be a large improvement since consecutive reads should already be cached, but it turns out to be somewhat faster anyway: 1.79s.

Note that for simplicity we now just discard the part of the sequence after the last segment of threads characters has been read. This is a negligible fraction of data so doesn’t affect the runtime significantly, but a proper implementation would have to deal with these last few characters separately.

V10: 1.79s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96
 L = 6
 assert D%L == 0
 DL = D//L
 threads = t*DL

 @cuda.jit(fastmath=True)
 def gpu_sketch(hashes, signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

     l = cuda.threadIdx.x
     k = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(2, tp1, D), dtype=nb.float32)

     Tin[0][k][l] = 0
     Tin[0][k+1][l] = 0
     Tin[1][k][l] = 0
     Tin[1][k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0][0] = 1
     Tin[1][0][0] = 1

     cuda.syncthreads()

     j = 0

+    local_seq = cuda.shared.array(shape=threads, dtype=nb.int32)
     # Loop over characters in the sequence.
+    tid = l + k * DL
+    assert tid < threads
+    for i in range((end-start)//threads):
+        idx = start + i*threads + tid
+        local_seq[tid] = seq[idx]
         cuda.syncthreads()

+        for c in local_seq:
+            if c == -1: break
+            assert c >= 0
+            assert c < A
+            h = hashes[c][k]
+            s = signs[c][k]
+            # Compute the shifted target index, avoiding a modulo operation.
+            for ll in range(L*l, L*(l+1)):
+                r = ll + h
+                r -= D if r >= D else 0
+                # Write to output tensor.
+                Tin[1-j][k+1][ll] = Tin[j][k+1][ll] + s * Tin[j][k][r]
+            j = 1-j
+            cuda.syncthreads()
+
+    # TODO: Handle leftover part of sequence
+
     # Copy to result.
     for ll in range(L*l, L*(l+1)):
         T[seqid][k+1][ll] = Tin[j][k+1][ll]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (l, k) <= (D, t)
         gpu_sketch[(blocks,1), (DL, t), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V11: Hashes and signs in shared memory

We can even copy the hashes ans signs from global to shared memory before using them. This again increases the amount of shared memory per block, which reduces the maximum number of blocks a single SM can run, but it turns out to be faster: 1.51s.

V11: 1.51s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96
 L = 6
 assert D%L == 0
 DL = D//L
 threads = t*DL

 @cuda.jit(fastmath=True)
+def gpu_sketch(global_hashes, global_signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

     l = cuda.threadIdx.x
     k = cuda.threadIdx.y
     assert k < t
     assert l < D

+    # Copy the global hashes/signs to shared memory.
+    hashes = cuda.shared.array(shape=(t, A), dtype=nb.int32)
+    signs = cuda.shared.array(shape=(t, A), dtype=nb.float32)
+    if l < A:
+        hashes[k][l] = global_hashes[k][l]
+        hashes[k][l] = global_hashes[k][l]
+
     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(2, tp1, D), dtype=nb.float32)

     Tin[0][k][l] = 0
     Tin[0][k+1][l] = 0
     Tin[1][k][l] = 0
     Tin[1][k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0][0] = 1
     Tin[1][0][0] = 1

     cuda.syncthreads()

     j = 0

     local_seq = cuda.shared.array(shape=threads, dtype=nb.int32)
     # Loop over characters in the sequence.
     tid = l + k * DL
     for i in range((end-start)//threads):
         idx = start + i*threads + tid
         local_seq[tid] = seq[idx]
         cuda.syncthreads()

         for c in local_seq:
             h = hashes[c][k]
             s = signs[c][k]
             # Compute the shifted target index, avoiding a modulo operation.
             for ll in range(L*l, L*(l+1)):
                 r = ll + h
                 r -= D if r >= D else 0
                 # Write to output tensor.
                 Tin[1-j][k+1][ll] = Tin[j][k+1][ll] + s * Tin[j][k][r]
             j = 1-j
             cuda.syncthreads()

     # TODO: Handle leftover part of sequence

     # Copy to result.
+    #for ll in range(L*l, L*(l+1)):
+    for ll in range(l, D, DL):
         T[seqid][k+1][ll] = Tin[j][k+1][ll]


 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (l, k) <= (D, t)
         gpu_sketch[(blocks,1), (DL, t), stream](self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

V12: Revisiting blocks per kernel

After playing around a bit, it seems that it’s now actually better to only send 4 sequences per kernel, instead of all of them. This gets the runtime down to 1.28s.

I’m not exactly sure why this is, but I suspect it has something to do with the fact that the block scheduler doesn’t always make optimal choices when the blocks are not of (roughly) the same size. Sending multiple kernels with fewer blocks is probably just a way to work around the suboptimal scheduling.

V13: Passing a tuple of sequences

Instead of concatenating multiple sequences into one longer sequence before passing them to the kernel, it would be nicer if we could just pass a list of sequences. Starting with version 0.53, Numba actually supports this, in a way. If we first copy all sequences to the device, we can then pass in a tuple of device sequences, and just take an index into that tuple in the kernel function.

Sadly, this actually generates slightly slower kernels than the sequence concatenation code, and I’m unsure why. The total runtime goes up to 1.39s.

It is expected that the host to device memory transfer is a bit slower in this case, since we now have to copy each sequence individually which creates more overhead, but it also seems to be that the kernels themselves run a bit slower. I’m hoping to find an answer in this Numba discourse post.

I’ve also seen a slowdown of up to 50% when using this technique, although this could be because of the increases memory transfer time instead of a kernel slowdown in itself.

V13: 1.39s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96
 L = 6
 assert D%L == 0
 DL = D//L
 threads = t*DL

 @cuda.jit(fastmath=True)
+def gpu_sketch(global_hashes, global_signs, seqs, T):

+    seq = seqs[cuda.blockIdx.x]
+    end = len(seq)

     l = cuda.threadIdx.x
     k = cuda.threadIdx.y
     assert k < t
     assert l < D

     # Copy the global hashes/signs to shared memory.
     hashes = cuda.shared.array(shape=(t, A), dtype=nb.int32)
     signs = cuda.shared.array(shape=(t, A), dtype=nb.float32)
     if l < A:
         hashes[k][l] = global_hashes[k][l]
         hashes[k][l] = global_hashes[k][l]

     # Shared memory for temporary DP tables.
     Tin = cuda.shared.array(shape=(2, tp1, D), dtype=nb.float32)


     Tin[0][k][l] = 0
     Tin[0][k+1][l] = 0
     Tin[1][k][l] = 0
     Tin[1][k+1][l] = 0

     cuda.syncthreads()

     Tin[0][0][0] = 1
     Tin[1][0][0] = 1

     cuda.syncthreads()

     j = 0

     local_seq = cuda.shared.array(shape=threads, dtype=nb.int32)
     # Loop over characters in the sequence.
     tid = l + k * DL
+    for i in range(end//threads):
+        idx = i*threads + tid
         local_seq[tid] = seq[idx]
         cuda.syncthreads()

         for c in local_seq:
             h = hashes[c][k]
             s = signs[c][k]
             # Compute the shifted target index, avoiding a modulo operation.
             for ll in range(L*l, L*(l+1)):
                 r = ll + h
                 r -= D if r >= D else 0
                 # Write to output tensor.
                 Tin[1-j][k+1][ll] = Tin[j][k+1][ll] + s * Tin[j][k][r]
             j = 1-j
             cuda.syncthreads()

     # TODO: Handle leftover part of sequence

     # Copy to result.
     #for ll in range(L*l, L*(l+1)):
     for ll in range(l, D, DL):
+        T[cuda.blockIdx.x][k+1][ll] = Tin[j][k+1][ll]

 class GTS:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

+        d_seqs = tuple(cuda.to_device(seq, stream=stream) for seq in seqs)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (l, k) <= (D, t)
+        gpu_sketch[(blocks,1), (DL, t), stream](self.d_hashes, self.d_signs, d_seqs, d_T)

         return d_T

V14: Better hardware

Instead of running on my years old laptop GPU, why not try some nicer hardware?

On a Titan X, the runtime is 0.98s.
On a 2080, the runtime is 0.50s.

Taking a closer look at the --analysis-metrics profile from the Titan X, we see the following: 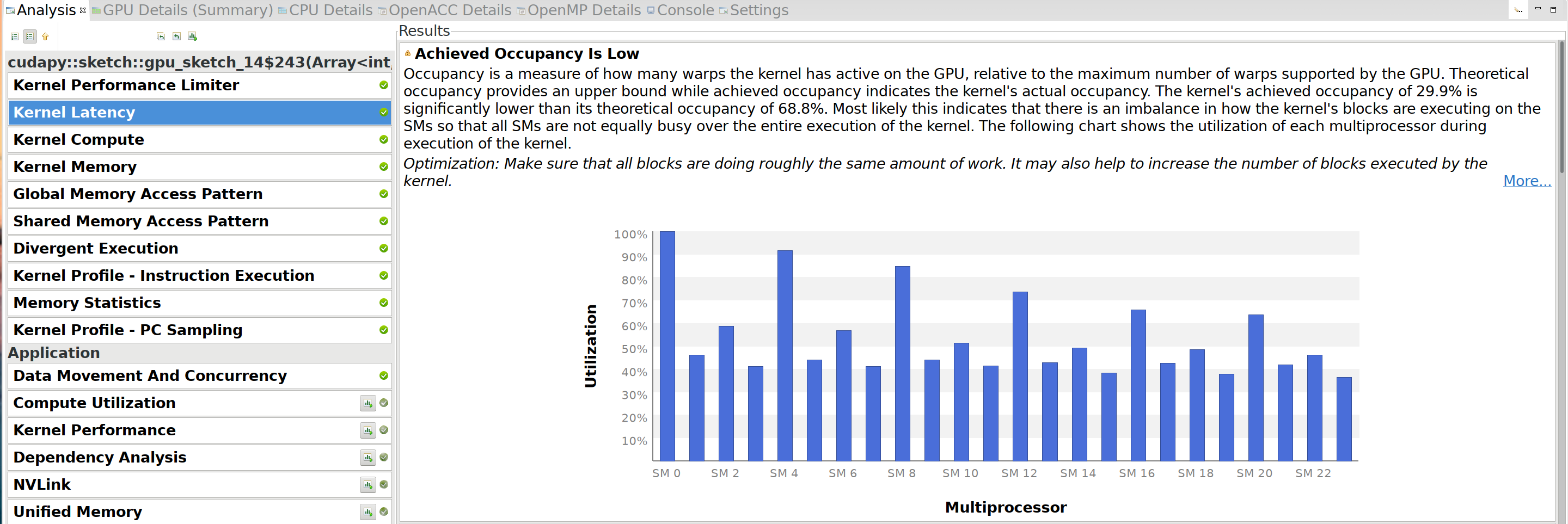This means that most multiprocessors are only busy for half the time. After some investigation, it turns out that the first SM is actually spending all it’s time processing one particularly long sequence. So if the data had been sequences of roughly equal length, the total throughput could have been twice faster.

Rerunning and profiling on the Titan X, but with homogeneous data so that all SMs have more than 95% utilization, we see that we’re close to maxing out the shared memory bandwidth:

We can also see that we’re getting very good performance on the 960M, using more than 70% of both compute and memory: 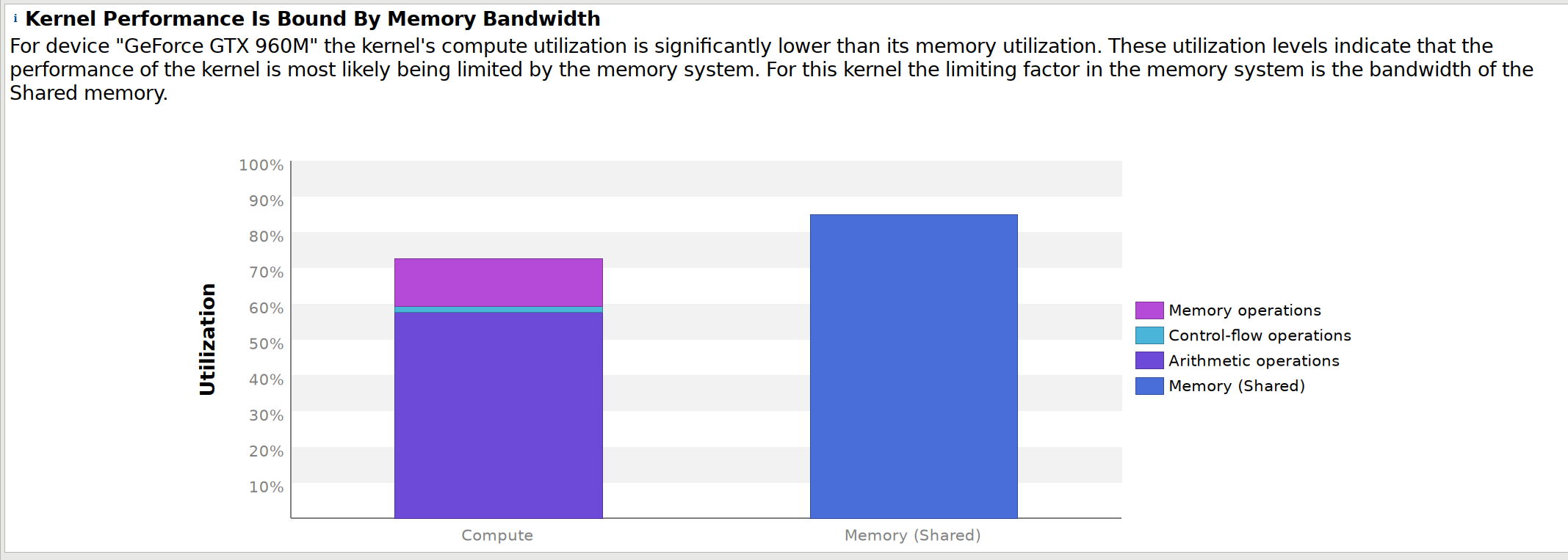These numbers are slightly lower for the Titan X, so it’s probably possible to do some more optimization for that specific card.

As a final thought, here’s the table showing the computation of the maximal number of warps per kernel (on the 960M again): 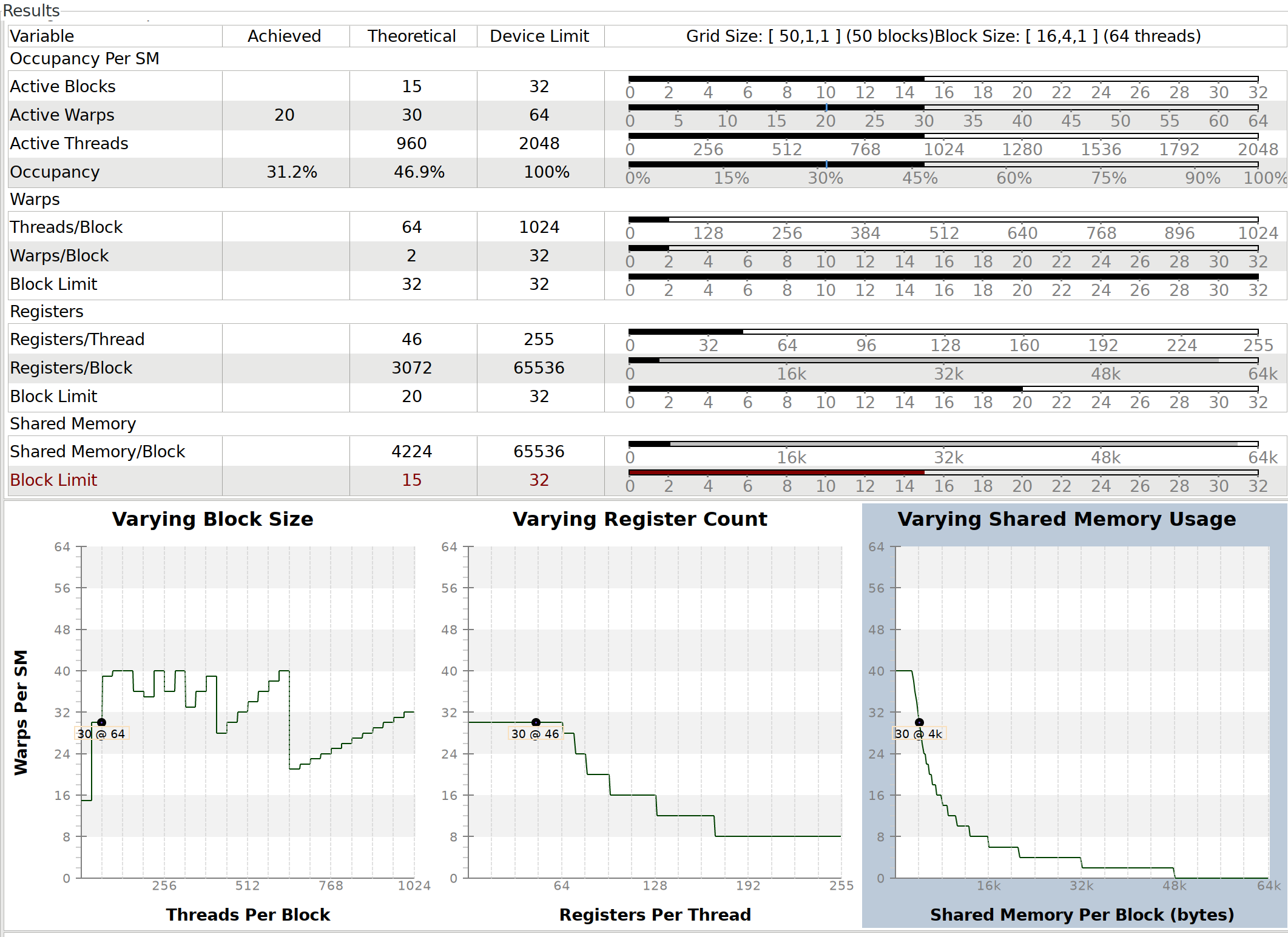According to this, we should be able to get a higher occupancy by reducing the shared memory per block. Currently each block uses 4224 bytes, so the 65KB shared memory per SM can only fit 15 blocks (of 2 warps each). This puts a limit of 30 active warps per SM, while the device limit it 64. One possibility could be to put the signs and hashes in read-only/constant memory, so the device can cache these more aggressively and we don’t have to spend shared memory on it, but this didn’t show an improvement in my testing.

V15: Dynamic shared memory

The current version of the code uses global (compile time) constants A, t, D, and L, and shared memory that is sized accordingly. It would be nicer if these were function arguments instead. To do this, we must use dynamic shared memory instead by passing the required size (in bytes) of the shared memory when starting the kernel.

gpu_sketch_15[(blocks,1), (DL, t), stream, 4*(2*tp1*D + 2*A*t + threads)](A, t, D, L, self.d_hashes, self.d_signs, d_seq, d_starts, d_T)
                                           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

The dynamic shared memory can be accessed by defining a shared memory variable with shape 0:

shared = cuda.shared.array(shape=0, dtype=nb.int32)

To make multiple shared memory arrays, the full dynamic shared memory can be sliced using the array[start:end] operator. It’s also possible to create arrays of different types by declaring the shared memory twice, with a different type. These arrays will be views into the same memory:

shared_i = cuda.shared.array(shape=0, dtype=nb.int32)
shared_f = cuda.shared.array(shape=0, dtype=nb.float32)

Tin = shared_f[0:2*tp1*D]
signs = shared_f[2*tp1*D:2*tp1*D+A*t]
hashes = shared_i[2*tp1*D+A*t:2*tp1*D+2*A*t]
local_seq = shared_i[2*tp1*D+2*A*t:2*tp1*D+2*A*t+threads]

Multidimensional dynamic shared memory is currently not supported, but can be emulated by manually computing indices into a linear array instead.

hashes[l*t+k] = global_hashes[l][k]
signs[l*t+k] = global_signs[l][k]

Using dynamic shared memory ends up being slower because it uses more registers to store all the array slices (62 vs 53), and changing the constants to function arguments further increases the number of registers to 96. This means that each SM can run much fewer threads in parallel, and hence the total throughput will be lower.

I tried playing around with the max_registers flag to @cuda.jit, but this didn’t provide any gains.

V15: 2.60s (Click to toggle)

 A = 4
 t = 4
 tp1 = t+1
 D = 96
 L = 6
 assert D%L == 0
 DL = D//L
 threads = t*DL

 @cuda.jit(fastmath=True)
+def gpu_sketch_15(A, t, D, L, global_hashes, global_signs, seq, starts, T):
     seqid = cuda.blockIdx.x
     start = starts[seqid]
     end = starts[seqid+1]

     l = cuda.threadIdx.x
     k = cuda.threadIdx.y
     assert k < t
     assert l < D

+    plane = tp1*D
+    threads = t*D//L

+    # NOTE: Tin has an offset of k*D to save a bit on further computations.
+    Tin = cuda.shared.array(shape=0, dtype=nb.float32)[k*D:2*plane]
+    local_seq = cuda.shared.array(shape=0, dtype=nb.int32)[2*plane:2*plane+threads]

+    signs = cuda.shared.array(shape=0, dtype=nb.float32)[2*plane+threads:2*plane+threads+A*t]
+    hashes = cuda.shared.array(shape=0, dtype=nb.int32)[2*plane+threads+A*t:2*plane+threads+2*A*t]
+
+    # Copy the global hashes/signs to shared memory.
+    if l < A:
+        hashes[l*t+k] = global_hashes[l][k]
+        signs[l*t+k] = global_signs[l][k]

+    for ll in range(l, D, D//L):
+        Tin[0*plane + 0*D + ll] = 0
+        Tin[0*plane + (0+1)*D + ll] = 0
+        Tin[1*plane + 0*D + ll] = 0
+        Tin[1*plane + (0+1)*D + ll] = 0

     cuda.syncthreads()

+    if k==0:
+        Tin[0] = 1
+        Tin[plane] = 1

     cuda.syncthreads()

     j = 0

     # Loop over characters in the sequence.
+    tid = l + k * D//L
     for i in range((end-start)//threads):
         idx = start + i*threads + tid
         local_seq[tid] = seq[idx]
         cuda.syncthreads()

         for c in local_seq:
+            h = hashes[c*t+k]
+            s = signs[c*t+k]
             # Compute the shifted target index, avoiding a modulo operation.
+            j2 = plane-j
             for ll in range(L*l, L*(l+1)):
                 r = ll + h
                 r -= D if r >= D else 0
                 # Write to output tensor.
+                Tin[j2 + D + ll] = Tin[j + D + ll] + s * Tin[j + r]

+            j = j2
+            cuda.syncthreads()

     # Copy to result.
+    for ll in range(l, D, D//L):
+        T[seqid][k][ll] = Tin[j +  ll]
+        T[seqid][k+1][ll] = Tin[j + D + ll]

+class GTS_15:
     def __init__(self):
         random.seed(31415)
         # An A*t array of random integers in [0, D)
         self.hashes = np.empty((A, t), dtype=np.int32)
         # An A*t array of random +-1
         self.signs  = np.empty((A, t), dtype=np.float32)
         for c in range(A):
             for k in range(t):
                 self.hashes[c][k] = random.randrange(0, D)
                 self.signs[c][k] = random.randrange(-1, 2, 2)

+        ts = TS_1()
+        self.hashes = np.array(ts.hashes, dtype=np.int32)
+        self.signs = np.array(ts.signs, dtype=np.float32)
+
         self.d_hashes = cuda.to_device(self.hashes)
         self.d_signs = cuda.to_device(self.signs)

     def sketch(self, seqs):
         # Allocate memory for the response.
         stream = cuda.stream()

         blocks = len(seqs)

         seq = np.concatenate(seqs)
         starts = np.array(np.cumsum(np.array([0] + [len(seq) for seq in seqs]), dtype=np.int32), dtype=np.int32)

         d_seq = cuda.to_device(seq, stream=stream)
         d_starts = cuda.to_device(starts, stream=stream)
         d_T = cuda.device_array((blocks, t+1, D), dtype=np.float32, stream=stream)

         # One thread per (l, k) <= (D, t)
+        gpu_sketch_15[(blocks,1), (DL, t), stream, 4*(threads+2*tp1*D+2*A*t)](np.int32(A), np.int32(t), np.int32(D), np.int32(L), self.d_hashes, self.d_signs, d_seq, d_starts, d_T)

         return d_T

Wrap up

At this point, we can safely stop optimizing. I was reminded that reading the file takes about a second as well - about as long as the processing itself, so there isn’t much point in going any further here. A gridsearch could still benefit from further improvements, or from using multiple GPUs on a single machine, but since performance is now limited by the longest sequence in the dataset, we can’t do much anyway without completely changing the algorithm.

Version	Time	Speedup
V0: original	~7 000s	1
V1: numba.jit	50s	140
Single threaded C++ code	50s	-
V2: multiprocessing	12s	580
V3: first GPU version	100s	70
V4: parallel kernels	13s	540
V5: more blocks per kernel	11s	650
V6: no fp64 operations	5.5s	1300
V7: less syncing	4.7s	1490
V8: shared mem access	4.6s	1520
V9: work per thread	1.88s	3700
V10: cache sequence	1.79s	3900
V11: cache hashes/signs	1.51	4600
V12: 4 blocks/kernel	1.28s	5500
V13: tuple of seqs	1.39s	8%-50% slower
V14a: Titan X	0.98s	7100
V14b: 2080	0.50s	20 000
V14c: Titan X, homogeneous data	~0.50s	14 000
V14d: 2080, homogeneous data	~0.25s	28 000
V15: dynamic shared memory	2.60s	2x slower