- 1 Introduction
- 2 Optimizing
find- 2.1 Linear
- 2.2 Auto-vectorization
- 2.3 Trailing zeros
- 2.4 Popcount
- 2.5 Manual SIMD
- 3 Optimizing the search
- 3.1 Batching
- 3.2 Prefetching
- 3.3 Pointer arithmetic
- 3.3.1 Up-front splat
- 3.3.2 Byte-based pointers
- 3.3.3 The final version
- 3.4 Skip prefetch
- 3.5 Interleave
- 4 Optimizing the tree layout
- 4.1 Left-tree
- 4.2 Memory layouts
- 4.3 Node size \(B=15\)
- 4.3.1 Data structure size
- 4.4 Summary
- 5 Prefix partitioning
- 5.1 Full layout
- 5.2 Compact subtrees
- 5.3 The best of both: compact first level
- 5.4 Overlapping trees
- 5.5 Human data
- 5.6 Prefix map
- 5.7 Summary
- 6 Multi-threaded comparison
- 7 Conclusion
- 7.1 Future work
- 7.1.1 Branchy search
- 7.1.2 Interpolation search
- 7.1.3 Packing data smaller
- 7.1.4 Returning indices in original data
- 7.1.5 Range queries
- 7.1.6 Sorting queries
- 7.1.7 Suffix array searching
- 7.1 Future work
In this post, we will implement a static search tree (S+ tree) for high-throughput searching of sorted data, as introduced on Algorithmica. We’ll mostly take the code presented there as a starting point, and optimize it to its limits. For a large part, I’m simply taking the ‘future work’ ideas of that post and implementing them. And then there will be a bunch of looking at assembly code to shave off all the instructions we can. Lastly, there will be one big addition to optimize throughput: batching.
All source code, including benchmarks and plotting code, is at github:RagnarGrootKoerkamp/static-search-tree.
Discuss on r/programming, hacker news, twitter, bsky, or youtube.
1 Introduction Link to heading
1.1 Problem statement Link to heading
Input. A sorted list of \(n\) 32bit unsigned integers vals: Vec<u32>.
Output. A data structure that supports queries \(q\), returning the smallest
element of vals that is at least \(q\), or u32::MAX if no such element exists.
Optionally, the index of this element may also be returned.
Metric. We optimize throughput. That is, the number of (independent) queries
that can be answered per second. The typical case is where we have a
sufficiently long queries: &[u32] as input, and return a corresponding answers: Vec<u32>.1
Note that we’ll usually report reciprocal throughput as ns/query (or just
ns), instead of queries/s. You can think of this as amortized (not average) time spent per query.
Benchmarking setup. For now, we will assume that both the input and queries are simply uniform random sampled 31bit integers2.
Code. In code, this can be modelled like this:
| |
1.2 Motivation Link to heading
Aside from doing this project just for the fun of it, there is some higher goal. One of the big goals of bioinformatics is to make efficient datastructures to index DNA, say a single human genome (3 billion basepairs/characters) or even a bunch of them. One such datastructure is the suffix array (wikipedia), that sorts the suffixes of the input string. Classically, one can then find the locations where a string occurs by binary searching the suffix array.
This project is a first step towards speeding up the suffix array search.
Also note that we indeed assume that the input data is static, since usually we use a fixed reference genome.
1.3 Recommended reading Link to heading
The classical solution to this problem is binary search, which we will briefly visit in the next section. A great paper on this and other search layouts is “Array Layouts for Comparison-Based Searching” by Khuong and Morin (2017). Algorithmica also has a case study based on that paper.
This post will focus on S+ trees, as introduced on Algorithmica in the followup post, static B-trees. In the interest of my time, I will mostly assume that you are familiar with that post.
I also recommend reading my work-in-progress introduction to CPU performance, which contains some benchmarks pushing the CPU to its limits. We will use the metrics obtained there as baseline to understand our optimization attempts.
Also helpful is the Intel Intrinsics Guide when looking into SIMD instructions.
Note that we’ll only be using AVX2 instructions here, as in, we’re assuming
intel. And we’re not assuming less available AVX512 instructions (in
particular, since my laptop doesn’t have them).
1.4 Binary search and Eytzinger layout Link to heading
As a baseline, we will use the Rust standard library binary search implementation.
| |
The main conclusion of the array layouts paper (Khuong and Morin 2017) is that the Eytzinger layout is one of the best in practice. This layout reorders the values in memory: the binary search effectively is a binary search tree on the data, with as root the middle node, then the nodes at positions \(\frac 14 n\) and \(\frac 34 n\), then \(\frac 18n, \frac 38n, \frac 58n, \frac 78n\), and so on. The main benefit of the Eytzinger layout is that all values needed for the first steps of the binary search are close together, so they can be cached efficiently: we put the root at index \(1\) and the two children of the node at index \(i\) are at \(2i\) and \(2i+1\). This means that we can effectively prefetch the next cache line, before knowing whether we need index \(2i\) or \(2i+1\). This can be taken a step further and we can prefetch the cache line containing indices \(16i\) to \(16i+15\), which are exactly the values needed 4 iterations from now. For a large part, this can quite effectively hide the latency associated with the traversal of the tree.
| |
If we plot these two, we see that Eytzinger layout performs as good as binary
search when the array fits in L2 cache (256kB for me, the middle red line), but starts to be much
better than binary search as the array grows to be much larger than the L3 cache (12MB).
In the end, Eytzinger search is around 4 times faster, which nicely corresponds
to being able to prefetch 4 iterations of cache lines from memory at a time.
Figure 1: Query throughput of binary search and Eytzinger layout as the size of the input increases. At 1GB input, binary search needs around 1150ns/query, while Eytzinger is 6x faster at 200ns/query. (I’m sorry for the two blue lines here. The top one is binary search and the bottom one Eytzinger. Getting all the plots to work took long enough, and customizing all the colours is annoying, so I’m just using cycling through the default colours. Unfortunately that ended up with two equal colours here. At least colours will be consistent from one plot to the next.)
1.5 Hugepages Link to heading
For all experiments, we’ll make sure to allocate the tree using 2MB hugepages
by default, instead of the usual 4kB pages.
This reduces pressure on the translation lookaside buffer (TLB) that
translates virtual memory addresses to hardware memory addresses, since its
internal table of pages is much smaller when using hugepages, and hence can be
cached better.
With transparent hugepages enabled, they are automatically given out whenever
allocating an exact multiple of 2MB, and so we always round up the allocation
for the tree to the next multiple of 2MB. However, it turns out that small
allocations below 32MB still go on the program’s heap, rather than asking
the kernel for new memory pages, causing them to not actually be hugepages.
Thus, all allocations we do are actually rounded up to the next multiple of
32MB instead.
All together, hugepages sometimes makes a small difference when the dataset is
indeed between 1MB and 32MB in size. Smaller data structures don’t really need
hugepages anyway. Enabling them for the Eytzinger layout as in the plot above
also gives a significant speedup for larger sizes.
1.6 A note on benchmarking Link to heading
The plots have the size of the input data on the logarithmic (bottom) x-axis. On the top,
they show the corresponding number of elements in the vector, which is 4 times
less, since each element is a u32 spanning 4 bytes.
Measurements are taken at values \(2^i\), \(1.25 \cdot 2^i\), \(1.5\cdot 2^i\), and
\(1.75\cdot 2^i\).
The y-axis shows measured time per query. In the plot above, it says
latency, since it is benchmarked as for q in queries { index.query(q); }.
Even then, the pipelining and out-of-order execution of the CPU will make it
execute multiple iterations in parallel. Specifically, while it is waiting for
the last cache lines of iteration \(i\), it can already start executing the first
instructions of the next query. To measure the true latency, we would have to
introduce a loop carried dependency by making query \(i+1\) dependent on the
result of query \(i\).
However, the main goal of this post is to optimize for throughput, so we won’t
bother with that.
Thus, all plots will show the throughput of doing index.query(all_queries).
For the benchmarks, I’m using my laptop’s i7-10750H CPU, with the frequency
fixed to 2.6GHz using Code Snippet 4.3
| |
2.6GHz.Also relevant are the sizes of the caches: 32KiB L1 cache per core, 256KiB
L2 cache per core, and 12MiB L3 cache shared between the physical 6 cores.
Furthermore, hyper-threading is disabled.
All measurements are done 5 times. The line follows the median, and we show the spread of the 2nd to 4th value (i.e., after discarding the minimum and maximum). Observe that in most of the plot above, the spread is barely visible! Thus, while especially the graph for binary search looks very noisy, that ’noise’ is in fact completely reproducible. Indeed, it’s caused by effects of cache associativity, as explained in the array layouts paper (Khuong and Morin (2017); this post is long enough already).
1.7 Cache lines Link to heading
Main memory and the caches work at the level of cache lines consisting of 64
bytes (at least on my machine), or 16 u32 values. Thus, even if you only read a single byte, if
the cache line containing that byte is not yet in the L1 cache, the entire thing
will be fetched from RAM or L3 or L2 into L1.
Plain binary search typically only uses a single value of each cache line, until it gets to the end of the search where the last 16 values span just 1 or 2 cache lines.
The Eytzinger layout suffers the same problem: even though the next cache line can be prefetched, it still only uses a single value in each. This fundamentally means that both these search schemes are using the available memory bandwidth quite inefficiently, and since most of what they are doing is waiting for memory to come through, that’s not great. Also, while that’s not relevant yet, when doing this with many threads in parallel, or with batching, single-core RAM throughput and the throughput of the main memory itself become a bottleneck.
It would be much better if somehow, we could use the information in each cache line much more efficiently ;)
We can do that by storing our data in a different way. Instead of storing it layer by layer, so that each iteration goes into a new layer, we can store 4 layers of the tree at a time (Code Snippet 5). That takes 15 values, and could nicely be padded into a full cache line. Then when we fetch a cache line, we can use it for 4 iterations at once – much better! On the other hand, now we can’t prefetch upcoming cache lines in advance anymore, so that overall the latency will be the same. But we fetch up to 4 times fewer cache lines overall, which should help throughput.
Unfortunately, I don’t have code and plots here, because what I really want to focus on is the next bit.
Figure 2: The first two rows show how we could pack four layers of the Eytzinger search into a single cache line. The first follows a classic binary search layout, while the second applies the Eytzinger layout recursively. The third row shows an S-tree node instead. For simplicity and clarity, I’m using consecutive values, but in practice, this would be any list of sorted numbers.
1.8 S-trees and B-trees Link to heading
We just ended with a node of 15 values that represent a height-4 search tree in which we can binary search. From there, it’s just a small step to S-trees.
B-trees. But first I have to briefly mention B-trees though (wikipedia). Those are the more classic dynamic variant, where nodes are linked together via pointers. As wikipedia writes, they are typically used with much larger block sizes, for example 4kB, since files read from disk usually come in 4kB chunks. Thus, they also have much larger branching factors.
S-trees. But we will instead use S-trees, as named so by Algorithmica. They are a nice middle ground between the high branching factor of B-trees, and the compactness of the Eytzinger layout. Instead of interpreting the 15 values as a search tree, we can also store them in a sorted way, and consider them as a 16-ary search tree: the 15 values simply split the data in the subtree into 16 parts, and we can do a linear scan to find which part to recurse into. But if we store 15 values and one padding in a cache line, we might as well make it 16 values and have a branching factor of 17 instead.
S+ trees. B-trees and S-trees only store each value once, either in a leaf node or in an internal node. This turns out to be somewhat annoying, since we must track in which layer the result was found. To simplify this, we can store all values as a leaf, and duplicate them in the internal nodes. This is then called a B+ tree or S+ tree. However, I will be lazy and just use S-tree to include this modification.
Figure 3: An example of a ‘full’ S+ tree (that I will from now just call S-tree) on 18 values with nodes of size (B=2) and branching factor (B+1=3). Each internal node stores the smallest value in the subtree on its right. In memory, the layers are simply packed together behind each other.
A full S-tree can be navigated in a way similar to the Eytzinger layout: The node (note: not4 value) at index \(i\) has its \(B+1\) child-nodes at indices \((B+1)\cdot i + 1 + \{0, \dots, B\}\).
When the tree is only partially filled, the full layout can waste a lot of space (Figure 4). Instead, we can pack the layers together, by storing the offset \(o_\ell\) of each layer.
The children of node \(o_\ell + i\) are then at \(o_{\ell+1} + (B+1)\cdot i + \{0, \dots, B\}\).
Figure 4: The full representation can be inefficient. The packed representation removes the empty space, and explicitly stores the offset (o_ell) where each layer starts.
At last, let’s have a look at some code. Each node in the tree is simply
represented as a list of \(N=16\) u32 values. We explicitly ask that nodes are
aligned to 64byte cache line boundaries.
| |
The S-tree itself is simply a list of nodes, and the offsets where each layer starts.
| |
To save some space, and focus on the interesting part (to me, at least), I will not show any code for constructing S-trees. It’s a whole bunch of uninteresting fiddling with indices, and takes a lot of time to get right. Also, construction is not optimized at all currently. Anyway, find the code here.
What we will look at, is code for searching S-trees.
| |
find function finds the index of the child of the current node.Our first step will be optimizing the find function.
2 Optimizing find
Link to heading
2.1 Linear Link to heading
Let’s first precisely define what we want find to do:
it’s input is a node with 16 sorted values and a query value \(q\), and it should return
the index of the first element that is at least \(q\).
Some simple code for this is Code Snippet 8.
| |
The results are not very impressive yet.
Figure 5: The initial version of our S-tree search is quite a bit slower than the Eytzinger layout. In this and following plots, ‘old’ lines will be dimmed, and the best previous and best new line slightly highlighted. Colours will be consistent from one plot to the next.
2.2 Auto-vectorization Link to heading
As it turns out, the early return; in Code Snippet 8 is really bad for performance,
since the branch predictor can’t do a good job on it.
Instead, we can count the number of values less than \(q\), and return that as the index of the first value \(\geq q\). (Example: all values \(\geq q\) index gives index 0.)
| |
if self.data[i] < q can be optimized into branchless code.In fact, the code is not just branchless, but actually it’s auto-vectorized into SIMD instructions!
| |
To save some space: you can find this and further results for this section in Figure 6 at the end of the section.
This auto-vectorized version is over two times faster than the linear find, and now clearly beats Eytzinger layout!
2.3 Trailing zeros Link to heading
We can also roll our own SIMD. The SIMD version of the original linear scan idea
does 16 comparisons in parallel, converts that to a bitmask, and then counts the
number of trailing zeros. Using #[feature(portable_simd)], that looks like this:
| |
find implementation using the count-trailing-zeros instruction. | |
popcntl, this ends with tzcntl.Now, let’s look at this generated code in a bit more detail.
First up: why does simd_le translate into min and cmpeq?
From checking the Intel Intrinsics Guide, we find out that there are only signed
comparisons, while our data is unsigned. For now, let’s just assume that all
values fit in 31 bits and are at most i32::MAX. Then, we can transmute our input
to Simd<i32, 8> without changing its meaning.
Both input values and queries are between 0 and i32::MAX.
Eventually we can fix this by either taking i32 input directly, or by shifting
u32 values to fit in the i32 range.
| |
| |
vpminud and vpcmpeqd instructions are gone now and merged into vpcmpgtd, but instead we got a vpxor back :/ (Ignore the different registers being used in the old versus the new version.)It turns out there is only a > instruction in SIMD, and not >=, and so there
is no way to avoid inverting the result.
We also see a vpshufd instruction that feels very out of place. What’s
happening is that while packing the result of the 16 u32 comparisons down to a
single 16bit value, data is interleaved in an unfortunate way, and we need to
fix that.
Here, Algorithmica takes the approach of ‘pre-shuffling’ the values in each
node to counter for the unshuffle instruction.
They also suggest using popcount instead, which is indeed what we’ll do next.
2.4 Popcount Link to heading
As we saw, the drawback of the trailing zero count approach is that the order of the lanes must be preserved. Instead, we’ll now simply count the number of lanes with a value less than the query, similar to the auto-vectorized SIMD before, so that the order of lanes doesn’t matter.
| |
| |
xor and or instructions are gone, but we are still stuck with the sequence of 5 instructions to go from the comparison results to an integer bitmask.Ideally we would like to movmsk directly on the u16x16 output of the first
pack instruction, vpackssdw, to get the highest bit of each of the 16 16-bit values.
Unfortunately, we are again let down by AVX2: there are movemask instructions
for u8, u32, and u64, but not for u16.
Also, the vpshufd instruction is now provably useless, so it’s slightly
disappointing the compiler didn’t elide it. Time to write the SIMD by hand instead.
2.5 Manual SIMD Link to heading
As it turns out, we can get away without most of the packing!
Instead of using vpmovmskb (_mm256_movemask_epi8) on 8bit data, we can
actually just use it directly on the 16bit output of vpackssdw!
Since the comparison sets each lane to all-zeros or all-ones, we can safely read
the most significant and middle bit, and divide the count by two at the
end.5
| |
[u32; 8], Simd<u32, 8> and the native __m256i type, but we'll have to live with it. | |
Now let’s have a look at the results of all this work.
Figure 6: Using the S-tree with an optimized find function improves throughput from 240ns/query for Eytzinger to 140ns/query for the auto-vectorized one, and down to 115ns/query for the final hand-optimized version, which is over 2x speedup!
As can be seen very nicely in this plot, each single instruction that we remove gives a small but consistent improvement in throughput. The biggest improvement comes from the last step, where we indeed shaved off 3 instructions.
In fact, we can analyse this plot a bit more:
- For input up to \(2^6=64\) bytes, the performance is constant, since in this case the ‘search tree’ only consists of the root node.
- Up to input of size \(2^{10}\), the tree has two layers, and the performance is constant.
- Similarly, we see the latency jumping up at size \(2^{14}\), \(2^{18}\), \(2^{22}\) and \(2^{26}\), each time because a new layer is added to the tree. (Or rather, the jumps are at powers of the branching factor \(B+1=17\) instead of \(2^4=16\), but you get the idea.)
- In a way, we can also (handwaivily) interpret the x-axis as time: each time the graph jumps up, the height of the jump is pretty much the time spent on processing that one extra layer of the tree.
- Once we exceed the size of L3 cache, things slow down quickly. At that point, each extra layer of the tree adds a significant amount of time, since waiting for RAM is inherently slow.
- On the other hand, once we hit RAM, the slowdown is more smooth rather than stepwise. This is because L3 is still able to cache a fraction of the data structure, and that fraction only decreases slowly.
- Again handwavily, we can also interpret the x-axis as a snapshot of space usage at a fixed moment in time: the first three layers of the tree fit in L1. The 4th and 5th layers fit in L2 and L3. Once the tree is 6 layers deep, the reads of that layer will mostly hit RAM, and any additional layers for sure are going to RAM.
From now on, this last version, find_popcnt, is the one we will be using.
3 Optimizing the search Link to heading
3.1 Batching Link to heading
As promised, the first improvement we’ll make is batching. Instead of processing one query at a time, we can process multiple (many) queries at once. This allows the CPU to work on multiple queries at the same time, and in particular, it can have multiple (up to 10-12) in-progress requests to RAM at a time. That way, instead of waiting for a latency of 80ns per read, we effectively wait for 10 reads at the same time, lowering the amortized wait time to around 8ns.
Batching very much benefits from the fact that we use an S+ tree instead of S-tree, since each element is found in the last layer (at the same depth), and hence the number of seach steps through the tree is the same for every element in the batch.
| |
Figure 7: Batch size 1 (red) performs very similar to our non-batched version (blue), around 115ns/query. Increasing the batch size to 2, 4, and 8 each time significantly improves performance, until it saturates at 45ns/query (2.5x faster) around 16.
One interesting observation is that going from batch size 1 to 2 does not double the performance. I suspect this is because the CPU’s out-of-order execution was already deep enough to effectively execute (almost) 2 queries in parallel anyway. Going to a batch size of 4 and then 8 does provide a significant speedup. Again going to 4 the speedup is relatively a bit less than when going to 8, so probably even with batch size 4 the CPU is somewhat looking ahead into the next batch of 4 already 🤯.
Throughput saturates at batch size 16 (or really, around 12 already), which corresponds to the CPU having 12 line fill buffers and thus being able to read up to 12 cache lines in parallel.
Nevertheless, we will settle on a batch size of 128, mostly because it leads to slightly cleaner plots in the remainder. It is also ever so slightly faster, probably because the constant overhead of initializing a batch is smaller when batches are larger.
3.2 Prefetching Link to heading
The CPU is already fetching multiple reads in parallel using out-of-order
execution, but we can also help out a bit by doing this explicitly using prefetching.
After processing a node, we determine the child node k that we need to visit
next, so we can directly request that node to be read from memory before
continuing with the rest of the batch.
| |
Figure 8: Prefetching helps speeding things up once the data does not fit in L2 cache anymore, and gets us down from 45ns/query to 30ns/query for 1GB input.
We observe a few things: first prefetching slightly slow things down while data fits in L1 already, since in that case the instruction just doesn’t do anything anyway. In L2, it makes the graph slightly more flat, indicating that already there, the latency is already a little bit of a bottleneck. In L3 this effect gets larger, and we get a nice smooth/horizontal graph, until we hit RAM size. There, prefetching provides the biggest gains.
3.3 Pointer arithmetic Link to heading
Again, it’s time to look at some assembly code, now to optimize the search function itself. Results are down below in Figure 9.
3.3.1 Up-front splat Link to heading
First, we can note that the find function splat’s the query from a u32 to
a Simd<u32, 8> on each call. It’s slightly nicer (but not really faster,
actually) to splat all the queries
up-front, and then reuse those.
| |
splat out of the loop is slightly nicer, but not faster.The assembly code for each iteration of the first loop now looks like this:
| |
3.3.2 Byte-based pointers Link to heading
Looking at the code above, we see two shlq $6 instructions that multiply the
given value by \(64\). That’s because our tree nodes are 64 bytes large, and
hence, to get the \(i\)’th element of the array, we need to read at byte \(64\cdot
i\). For smaller element sizes, there are dedicated read instructions that
inline, say, an index multiplication by 8. But for a stride of 64, the compiler
has to generate ‘manual’ multiplications in the form of a shift.
Additionally, direct pointer-based lookups can be slightly more efficient here than
array-indexing: when doing self.tree[o + k[i]], we can effectively pre-compute
the pointer to self.tree[o], so that only k[i] still has to be added. Let’s
first look at that diff:
| |
Now, we can avoid all the multiplications by 64, by just multiplying all k[i]
by 64 to start with:
| |
Indeed, the generated code now goes down from 17 to 15 instructions, and we can see in Figure 9 that this gives a significant speedup!
| |
3.3.3 The final version Link to heading
One particularity about the code above is the andl $-64,%r9d.
In line 6, the bitmask gets written there. Then in line 7, it’s popcounted.
Line 11 does a shll $5, i.e., a multiplication by 32, which is a combination
of the /2 to compensate for the double-popcount and the * 64. Then, it does
the and $-64, where the mask of -64 is 111..11000000 which ends in 6 zeros.
But we just multiplied by 32, so all this does is zeroing out a single bit, in
case the popcount was odd. But we know for a fact that that can never be, so we
don’t actually need this and instruction.
To avoid it, we do this /2*64 => *32 optimization manually.
| |
/2 and *64 into *32.Again, this gives a small speedup.
Figure 9: Results of improving the search function bit by bit. Like before, the improvements are small but consistent. Throughput on 1GB input improves from 31ns/query to 28ns/query.
3.4 Skip prefetch Link to heading
Now we know that the first three levels of the graph fit in L1 cache, so probably we can simply skip prefetching for those levels.
Figure 10: Skipping the prefetch for the first layers is slightly slower.
As it turns out, skipping the prefetch does not help. Probably because the prefetch is cheap if the data is already available, and there is a small chance that the data we need was evicted to make room for other things, in which case the prefetch is useful.
3.5 Interleave Link to heading
One other observation is that the first few layers are CPU bound, while the last few layers are memory throughput bound. By merging the two domains, we should be able to get a higher total throughput. (Somewhat similar to how for a piece wise linear convex function \(f\), \(f((x+y)/2) < (f(x)+f(y))/2\) when \(x\) and \(y\) are on different pieces.) Thus, maybe we could process two batches of queries at the same time by processing layer \(i\) of one batch at the same time as layer \(i+L/2\) of the other batch (where \(L\) is the height of the tree). I implemented this, but unfortunately the result is not faster than what we had.
Or maybe we can split the work as: interleave the last level of one half with all but the last level of the other half? Since the last-level memory read takes most of the time. Also that turns out slower in practice.
What does give a small speedup: process the first two levels of the next batch
interleaved with the last prefetch of the current batch. Still the result is
only around 2ns speedup, while code the (not shown ;") gets significantly more
messy.
What does work great, is interleaving all layers of the search: when the tree has \(L\) layers, we can interleave \(L\) batches at a time, and then process layer \(i\) of the \(i\)’th in-progress batch. Then we ‘shift out’ the completed batch and store the answers to those queries, and ‘shift in’ a new batch. This way, we completely average the different workloads of all the layers, and should achieve near-optimal performance given the CPU’s memory bandwidth to L3 and RAM (at least, that’s what I assume is the bottleneck now).
Click to show code for interleaving.
| |
Figure 11: Interleaving all layers of the search binary search improves throughput from 29ns/query to 24ns/query.
4 Optimizing the tree layout Link to heading
4.1 Left-tree Link to heading
So far, every internal node of the tree stores the minimum of the subtree on it’s right (Figure 3, reproduced below).
Figure 12: Usually in B+ trees, each node stores the minimum of it’s right subtree. Let’s call this a right (S+/B+) tree.
This turns out somewhat inefficient when searching values that are exactly in between two subtrees (as also already suggested by Algorithmica), such as \(5.5\). In that case, the search descends into the leftmost (green) subtree with node \([2, 4]\). Then, it goes to the rightmost (red) node \([4,5]\). There, we realize \(5.5 > 5\), and thus we need the next value in the red layer (which is stored as a single array), which is \(6\). The problem now is that the red tree nodes exactly correspond to cache lines, and thus, the \(6\) will be in a new cache line that needs to be fetched from memory.
Now consider the left-max tree below:
Figure 13: In the left-max S+ tree, each internal node contains the maximum of its left subtree.
Now if we search for \(5.5\), we descend into the middle subtree rooted at \([7,9]\). Then we go left to the \([6,7]\) node, and end up reading \(6\) as the first value \(\geq 5.5\). Now, the search directly steers toward the node that actually contains the answer, instead of the one just before.
Figure 14: The left-S tree brings runtime down from 24ns/query for the interleaved version to 22ns/query now.
4.2 Memory layouts Link to heading
Let’s now consider some alternative memory layouts. So far, we were packing all layers in forward order, but the Algorithmica post actually stores them in reverse, so we’ll try that too. The query code is exactly the same, since the order of the layers is already encoded into the offsets.
Another potential improvement is to always store a full array. This may seem very inefficient, but is actually not that bad when we make sure to use uninitialized memory. In that case, untouched memory pages will simply never be mapped, so that we waste on average only about 2MB per layer when hugepages are enabled, and 14MB when there are 7 layers and the entire array takes 1GB.
Figure 15: So far we have been using the packed layout. We now also try the reversed layout as used by Algorithmica, and the full layout that allows simple arithmetic for indexing.
A benefit of storing the full array is that instead of using the offsets, we can simply compute the index in the next layer directly, as we did for the Eytzinger search.
| |
Figure 16: Comparison with reverse and full memory layout, and full memory layout with using a dedicated _full search that computes indices directly.
As it turns out, neither of those layouts improves performance, and so we will not use them going forward.
4.3 Node size \(B=15\) Link to heading
We can also try storing only 15 values per node, so that the branching factor
is 16. This has the benefit of making the multiplication by \(B+1\) (17 so far)
slightly simpler, since it replaces x = (x<<4)+x by x = x<<4.
Figure 17: Storing 15 values per node. The lines in the bottom part of the plot show the overhead that each data structure has relative to the size of the input, capped at 1 (which corresponds to take double the size).
When the tree has up to 5 layers and the data fits in L3 cache, using \(B=15\) is indeed slightly faster when the number of layers in the tree is the same. On the other hand, the lower branching factor of \(16\) requires an additional layer for smaller sizes than when using branching factor \(17\). When the input is much larger than L3 cache the speedup disappears, because RAM throughput becomes a common bottleneck.
4.3.1 Data structure size Link to heading
Plain binary search and the Eytzinger layout have pretty much no overhead. Our S+ tree so far has around \(1/16=6.25\%\) overhead: \(1/17\) of the values in the final layer is duplicated in the layer above, and \(1/17\) of those is duplicated again, and so on, for a total of \(1/17 + 1/17^2 + \cdots = 1/16\).
Using node size \(15\) instead, increases the overhead: Each node now only stores \(15\) instead of \(16\) elements, so that we already have an overhead of \(1/15\). Furthermore the reduced branching factor increases the duplication overhead from \(1/16\) to \(1/15\) as well, for a total overhead of \(2/15 = 13.3\%\), which matches the dashed blue line in Figure 17.
4.4 Summary Link to heading
Figure 18: A summary of all the improvements we made so far.
Of all the improvements so far, only the interleaving is maybe a bit too much: it is the only method that does not work batch-by-batch, but really benefits from having the full input at once. And also its code is three times longer than the plain batched query methods because the first and last few iterations of each loop are handled separately.
5 Prefix partitioning Link to heading
So far, we’ve been doing a purely comparison-based search. Now, it is time for something new: partitioning the input values.
The simplest form of the idea is to simply partition values by their top \(b\) bits, into \(2^b\) parts. Then we can build \(2^b\) independent search trees and search each query in one of them. If \(b=12\), this saves the first two levels of the search (or slightly less, actually, since \(2^{12} = 16^3 < 17^3\)).
5.1 Full layout Link to heading
In memory, we can store these trees very similar to the full layout we had before, with the main differences that the first few layers are skipped and that now there will be padding at the end of each part, rather than once at the end.
Figure 19: The full partitioned layout concatenates the full trees for all parts ‘horizontally’. As a new detail, when a part is not full, the smallest value of the next part is appended in the leaf layer.
For some choices of \(b\), it could happen that up to \(15/16\) of each tree is padding. To reduce this overhead, we attempt to shrink \(b\) while keeping the height of all trees the same: as long as all pairs of adjacent trees would fit together in the same space, we decrease \(b\) by one. This way, all parts will be filled for at least \(50\%\) when the elements are evenly distributed.
Once construction is done, the code for querying is very similar to before: we
only have to start the search for each query at the index of its part, given by
q >> shift for some value of shift, rather than at index \(0\).
| |
Figure 20: The ‘simple’ partitioned tree, for (b_{textrm{max}}in {4,8,12,16,20}), shown as dotted lines.
We see that indeed, the partitioned tree has a space overhead varying between \(0\) and \(1\), making this not yet useful in practice. Larger \(b\) reduce the height of the remaining trees, and indeed we see that queries are faster for larger \(b\). Especially for small trees there is a significant speedup over interleaving. Somewhat surprisingly, none of the partition sizes has faster queries than interleaving for large inputs. Also important to note is that while partitioning is very fast for sizes up to L1 cache, this is only possible because they have \(\gg 1\) space overhead.
5.2 Compact subtrees Link to heading
Just like we used the packed layout before, we can also do that now, by simply concatenating the representation of all packed subtrees. We ensure that all subtrees are still padded into the same total size, but now we only add as much padding as needed for the largest part, rather than padding to full trees. Then, we give each tree the same layout in memory.
We’ll have offsets \(o_\ell\) of where each layer starts in the first tree, and we store the constant size of the trees. That way, we can easily index each layer of each part.
Figure 21: Compared to before, Figure 19, the lowest level of each subtree now only takes 2 instead of 3 nodes.
The code for querying does become slightly more complicated. Now, we must
explicitly track the part that each query belongs to, and compute all indices
based on the layer offset, the in-layer offset k[i], and the part offset.
| |
Figure 22: Compared to the the simple/full layout before (dark blue dots for (b=16)), the compact layout (e.g. red dots for (b=16)) consistently uses less memory, but is slightly slower.
For fixed \(b_{\textrm{max}}\), memory overhead of the compact layout is small as long as the input is sufficiently large and the trees have sufficiently many layers. Thus, this tree could be practical. Unfortunately though, querying them is slightly slower than before, because we must explicitly track the part of each query.
5.3 The best of both: compact first level Link to heading
As we just saw, storing the trees one by one slows queries down, so we would like to avoid that. But on the other hand, the full layout can waste space.
Here, we combine the two ideas. We would like to store the horizontal concatenation of the packed trees (each packed to the same size), but this is complicated, because then levels would have a non-constant branching factor. Instead, we can fully omit the last few (level 2) subtrees from each tree, and pad those subtrees that are present to full subtrees. This way, only the first level has a configurable branching factor \(B_1\), which we can simply store after construction is done.
This layout takes slightly more space than before because the subtrees must be full, but the overhead should typically be on the order of \(1/16\), since (for uniform data) each tree will have \(\geq 9\) subtrees, of which only the last is not full.
Figure 23: We can also store the horizontal concatenation of all trees. Here, the number of subtrees can be fixed to be less than (B+1), and is (2) instead of (B+1=3). Although not shown, deeper layers must always be full and have a (B+1) branching factor.
| |
self.b1 instead of B+1 there.Figure 24: When compressing the first level, space usage is very similar to the compact layout before, and query speed is as fast as the full layout before.
5.4 Overlapping trees Link to heading
A drawback of all the above methods is that memory usage is heavily influenced by the largest part, since all parts must be at least as large. This is especially a problem when the distribution of part sizes is very skewed. We can avoid this by sharing storage between adjacent trees. Let \(S_p\) be the number of subtrees for each part \(p\), and \(S_{max} = \max_p S_p\). Then, we can define the overlap \(0\leq v\leq B\), and append only \(B_1 = S_{max}-v\) new subtrees for each new part, rather than \(S_{max}\) as we did before. The values for each part are then simply appended where the previous part left off, unless that subtree is ‘out-of-reach’ for the current part, in which case first some padding is added. This way, consecutive parts can overlap and exchange memory, and we can somewhat ‘buffer’ the effect of large parts.
Figure 25: In this example, the third tree has (6) values in ([8, 12)) and requires (S_{max}=3) subtrees. We have an overlap of (v=1), so that for each additional tree, only (2) subtrees are added. We add padding elements in grey to ensure all elements are reachable from their own tree.
When the overlap is \(1\), as in the example above, the nodes in the first layer each contain the maximum value of \(B\) subtrees. When the overlap is larger than \(1\), the nodes in the first layer would contain overlapping values. Instead, we store a single list of values, in which we can do unaligned reads to get the right slice of \(B\) values that we need.
| |
read_unaligned since we do not always read at 16-value boundaries anymore.Figure 26: Overlapping trees usually use less memory than the equivalent version with first-level compression, while being about as fast.
5.5 Human data Link to heading
So far we’ve been testing with uniform random data, where the largest part
deviates form the mean size by around \(\sqrt n\). Now, let’s look at some real
data: k-mers of a human genome. DNA consists of ACGT characters that can be
encoded as 2 bits, so each string of \(k=16\) characters defines a 32 bit
integer6.
We then look at the first \(n\) k-mers of the human genome, starting at chromosome 1.
To give an idea, the plot below show for each k-mer of length \(k=12\) how often it occurs in the full human genome. In total, there are around 3G k-mers, and so the expected count for each k-mer is around 200. But instead, we see k-mers that occur over 2 million times! So if we were to partition on the first 24 bits, the size of the largest part is only around \(2^{-10}\) of the input, rather than \(2^{-24}\).
The accumulated counts are shown in orange, where we also see a number of flat regions caused by underrepresented k-mers.
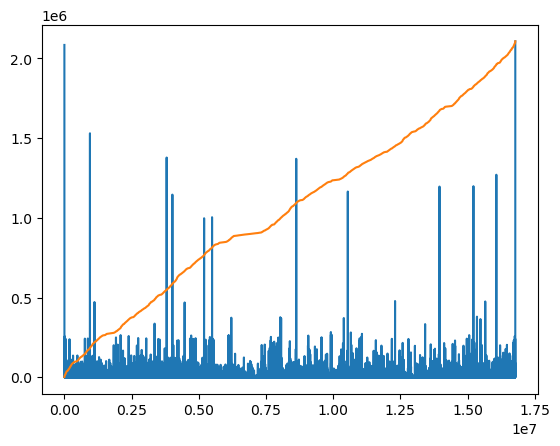
Figure 27: A plot showing k-mer counts for all (4^{12} = 16M) $k=12$-mers of the human genome. On random data each k-mer would occur around 200 times, but here we see some k-mers occurring over 2 million times.
Figure 28: Building the overlapping trees for k-mers of the human genome takes much more space, and even using only 16 parts regularly requires up to 50% overhead, making this data structure not quite practical.
5.6 Prefix map Link to heading
We need a way to handle unbalanced partition sizes, instead of mapping everything linearly. We can do this by simply storing the full tree compactly as we did before, preceded by an array (in blue below) that points to the index of the first subtree containing elements of the part. Like for the overlapping trees before, the first layer is simply a list of the largest elements of all subtrees that can be indexed anywhere (potentially unaligned).
Figure 29: The prefix map, in blue, stores (2^b) elements, that for each $b$-bit prefix stores the index of the first subtree that contains an element of that prefix.
To answer a query, we first find its part, then read the block (16 elements) starting at the pointed-to element, and then proceed as usual from the sub-tree onward.
| |
prefix_map to jump directly to the right place in the packed tree representation.Figure 30: As long as there are more elements than parts and the tree has at least two layers, the space overhead of this representation is close to (1/16) again.
Although memory usage is now similar to the unpartitioned version, queries for large inputs are slightly slower than those previous layouts due to the additional index required.
We can also again do the interleaving queries. These are slightly faster for small inputs, and around as fast as interleaving was without the partitioning.
Figure 31: Prefix-map index with interleaving queries on random data.
On human data, we see that the partitioned index is a bit faster in L1 and L2, and consistently saves the time of roughly one layer in L3. For larger indices, performance is still very similar to not using partitioning at all.
Figure 32: Prefix-map with interleaving on human data.
5.7 Summary Link to heading
Figure 33: Summary of partitioning results. Overall, it seems that partitioning does not provide when we already interleave queries.
6 Multi-threaded comparison Link to heading
Figure 34: When using 6 threads, runtime goes down from 27ns to 7ns. Given that the speedup is less than 4x, we are now bottlenecked by total RAM throughput, and indeed methods that are slower for a single thread also reach near-optimal throughput now.
7 Conclusion Link to heading
All together, we went from 1150ns/query for binary search on 4GB input to
27ns for the optimized S-tree with interleaved queries, over 40x speedup!
A large part of this improvement is due to batching queries and prefetching
upcoming nodes. To get even higher throughput, interleaving queries at different
levels helps to balance the CPU-bound part of the computation with the
memory-bound part, so that we get a higher overall throughput. Using a 15
elements per node instead of 16 also improves throughput somewhat, but doubles
the overhead of the data structure from 6.25% to 13.3%. For inputs that fit in
L3 cache that’s fine and the speedup is worthwhile, while for larger inputs the
speed is memory-bound anyway, so that there is no speedup while the additional
memory requirements are somewhat large.
We also looked into partitioning the data by prefix. While this does give some speedup, it turns out that on skewed input data, the benefits quickly diminish since the tree either requires a lot of buffer space, or else requires an additional lookup to map each part to its location in the first level of the tree. In the end, I’d say the additional complexity and dependency on the shape of the input data of partitioning is not worth the speedup compared to simply using interleaved queries directly.
7.1 Future work Link to heading
7.1.1 Branchy search Link to heading
All methods we considered are branchless and use the exact same number of iterations for each query. Especially in combination with partitioning, it may be possible to handle the few large parts independently from the usual smaller parts. That way we could answer most queries with slightly fewer iterations.
On the other hand, the layers saved would mostly be the quick lookups near the root of the tree, and introducing branches to the code could possibly cause quite a bit of delay due to mispredictions.
7.1.2 Interpolation search Link to heading
As we saw in the last plot above, total RAM throughput (rather than per-core throughput) becomes a bottleneck once we’re using multiple threads. Thus, the only way to improve total query throughput is to use strictly fewer RAM accesses per query. Prefix lookups won’t help, since they only replace the layers of the tree that would otherwise fit in the cache. Instead, we could use interpolation search (wikipedia), where the estimated position of a query \(q\) is linearly interpolated between known positions of surrounding elements. On random data, this only takes \(O(\lg \lg n)\) iterations, rather than \(O(\lg n)\) for binary search, and could save some RAM accesses. On the other hand, when data is not random its worst case performance is \(O(n)\) rather than the statically bounded \(O(\lg n)\).
The PLA-index (Abrar and Medvedev 2024) also uses a single interpolation step in a precisely constructed piece wise linear approximation. The error after the approximation is determined by some global upper bound, so that the number of remaining search steps can be bounded as well.
7.1.3 Packing data smaller Link to heading
Another option to use the RAM lookups more efficiently would be to pack values into 16 bits rather than the 32 bits we’ve been using so far. Especially if we first do a 16 bit prefix lookup, we already know those bits anyway, so it would suffice to only compare the last 16 bits of the query and values. This increases the branching factor from 17 to 33, which reduces the number of layers of the tree by around 1.5 for inputs of 1GB.
Another option, also suggested by ant6n on hacker news, would be some kind of ‘variable depth’ encoding, where the root node stores, say, the top 16 bits of every value, and as we go down the tree, we store some ‘middle’ 16 bits, skipping the first \(p\) bits that are shared between all elements in the bucket.
7.1.4 Returning indices in original data Link to heading
For various applications, it may be helpful to not only return the smallest value \(\geq q\), but also the index in the original list of sorted values, for example when storing an array with additional data for each item.
Since we use the S+ tree that stores all data in the bottom layer, this is mostly straightforward. The prefix map partitioned tree also natively supports this, while the other partitioned variants do not: they include buffer/padding elements in their bottom layer, and hence we would need to store and look up the position offset of each part separately.
7.1.5 Range queries Link to heading
We could extend the current query methods to a version that return both the first value \(\geq q\) and the first value \(>q\), so that the range of positions corresponding to value \(q\) can be determined. In practice, the easiest way to do this is by simply doubling the queries into \(q\) and \(q+1\). This will cause some CPU overhead in the initial layers, but the query execution will remain branch-free. When \(q\) is not found or only occurs a few times, they will mostly fetch the same cache lines, so that memory is efficiently reused and the bandwidth can be used for other queries.
In practice though, this seems only around 20% faster per individual query for 4GB input, so around 60% slower for a range than for a single query. For small inputs, the speedup is less, and sometimes querying ranges is even more than twice slower than individual random queries.
7.1.6 Sorting queries Link to heading
Another thing that we did not at all consider so far, but was brought up by orlp on hacker news, is to batch queries. If we assume for the moment that the queries are sorted, we know that we have maximal possible reusing of all nodes, and they all need to be fetched from memory only once. If the number of queries is large (say at least \(n/16\)) then many nodes at the last level will have more than one query hitting them, and fetching them only once will reduce memory pressure. Similarly, if we have at least around \(n/256\) queries, we can avoid fetching before-last layer nodes multiple times.
In practice, I’m not quite sure how much time the sorting of queries would take, but something simple would be to do one or two rounds of 8-bit radix sort, so we sort into \(256=16^2\) or \(65536=16^4\) parts, and we can then skip the first two or four first layers of the search.
7.1.7 Suffix array searching Link to heading
The next step of this project is to integrate this into a fast suffix array (wikipedia) search scheme. The idea is to build this S-tree on, say, every 4th suffix, and then use the first 32 bits (or maybe 64) of each suffix as the value in the S-tree. Given a query, we can then quickly determine the range corresponding to its first 32 bits, and binary search only in the (likely small) remaining range to determine the final slice of the suffix array that corresponds to the query.
References Link to heading
For those not familiar with Rust syntax,
Vec<u32>is simply an allocated vector of 32 bit unsigned integers, likestd::vectorin C++.&[u32]is a slice (or view) pointing to some non-owned memory.[u32; 8]is an array of 8 elements, likestd::array<unsigned int, 8>. ↩︎You’ll see later why not 32bit ↩︎
One might argue that this is unrealistic since in practice processors do have dynamic frequencies, but here I prefer reproducible benchmarks over realistic benchmarks. ↩︎
;) ↩︎
It would be really cool if we could teach compilers this trick. It already auto-vectorized the counting code anyway, so this is not that much more work I’d say. ↩︎
We throw away the most significant bit to get 31 bit values. ↩︎