These are some notes about linear time suffix array (SA) construction algorithms (SACA’s).
- At the bottom you can find a visualization.
- This page has an interactive demo.
History of suffix array construction algorithms:
- 1990 first algorithm: Manber and Myers (1993)
- 2002 small/large suffixes, explained below: Ko and Aluru (2005)
- 2009 recursion only on LMS suffixes: Nong, Zhang, and Chan (2009)
These slides from Stanford are a nice reference for the last algorithm.
Notation Link to heading
- String \(S = s_0\dots s_{n-1}s_n\).
- $s_n=\$$ is the sentinel, smaller than all other characters.
- Suffix from \(i\): \(S_i := s_i\dots s_n\).
- \(i\) indexes the string \(S\).
- \(j\) indexes the suffix array \(A\).
- Let \(P_i\) be the position of suffix \(S_i\) in the suffix array.
- \(A_{P_i} = i\) and \(P_{A_j}=j\) by definition.
- The previous-suffix and next-suffix of \(S_i\) are \(S_{i-1}\) and \(S_{i+1}\) respectively.
Small and Large suffixes Link to heading
- Suffix \(S_i\) is small (S-suffix) when \(S_i < S_{i+1}\). \(S_n\) is small by definition.
- Suffix \(S_i\) is large (L-suffix) when \(S_i > S_{i+1}\).
- Equality isn’t possible because of the sentinel.
Then by definition:
- when \(S_i\) is small: \(P_i < P_{i+1}\), ie S-suffixes come before their next-suffix.
- when \(S_i\) is large: \(P_i > P_{i+1}\), ie L-suffixes come after their next-suffix.
Lemma 1: When an S-suffix and L-suffix start with the same character \(c\), the L-suffix comes before the S-suffix in the suffix array.
Proof:
- The S-suffix is of the form $c^x d …$, with \(d>c\) and \(x>0\).
- The L-suffix is of the form $c^y b …$, with \(b<c\) and \(y>0\).
- Since \(b<c<d\), no matter what \(x\) and \(y\) are, the L-suffix is less than the S-suffix.
Building the suffix array from a smaller one Link to heading
It turns out we can build the SA of \(S\) once we know the SA-order of all small suffixes.
Lemma 2: The set of L-suffixes $\{S_i : s_i =c \text{ and $S_i$ is large }\}$ starting with the same character \(c\) occurs in the same order in the SA as the corresponding next-suffixes \(S_{i+1}\).
Proof: This follows simply from the fact that a set of strings starting with \(c\) can be sorted by only comparing them from the second character onward.
Extension algorithm: This gives the following algorithm to build \(A\) from the partial suffix array of small suffixes:
- Start by initializing a bucket for each character \(c\) in \(S\): Determine the position in \(A\) of the first and last suffix starting with \(c\) by counting the number of characters in \(S\) that are \(<c\) and \(\leq c\) respectively.
- By Lemma 1, the S-suffixes starting with character \(c\) come after the L-suffixes starting with \(c\), and hence can be copied in their already-sorted order to the end of bucket \(c\).
- Now we iterate over the suffix array position \(j\) from \(0\) to \(n\) to fill in the large suffixes in the right places. Recall that \(S_{A_j}\) is the suffix at position \(j\) of the suffix array, and \(S_{A_j-1}\) is its previous-suffix. Also, \(A_0 = n\) by definition, since $S_n = \$$ is minimal.
- If the previous-suffix \(S_{A_j-1}\) is small, it is smaller than \(S_{A_j}\) and hence already positioned at a smaller position \(j’ = P_{A_j-1} < j\).
- If the previous-suffix \(S_{A_j-1}\) is large, this is the next-smallest
suffix starting with character \(c=s_{A_j-1}\). Indeed, by Lemma 2, any smaller
L-suffix starting with \(c\) has a smaller next-suffix, which has been
processed already (seen at position \(< j\)), while any larger L-suffix has a larger next-suffix, which
has not been processed already (not seen at position \(\leq j\)).
Write \(A_j-1\) to the first empty slot in the bucket for \(c\).
Once \(j\) reaches \(n\), this algorithm has completely filled in \(A\). Note that it can never run into empty slots.1
Visualization Link to heading
I wrote a small visualizer for the algorithm above, see this repo and this post. You can use it to visualize the algorithm for any input string.
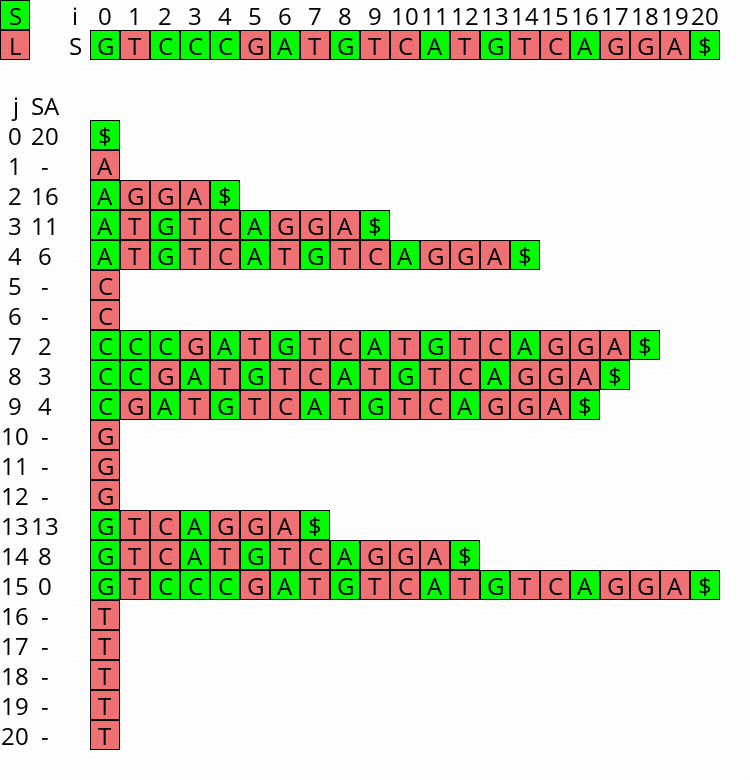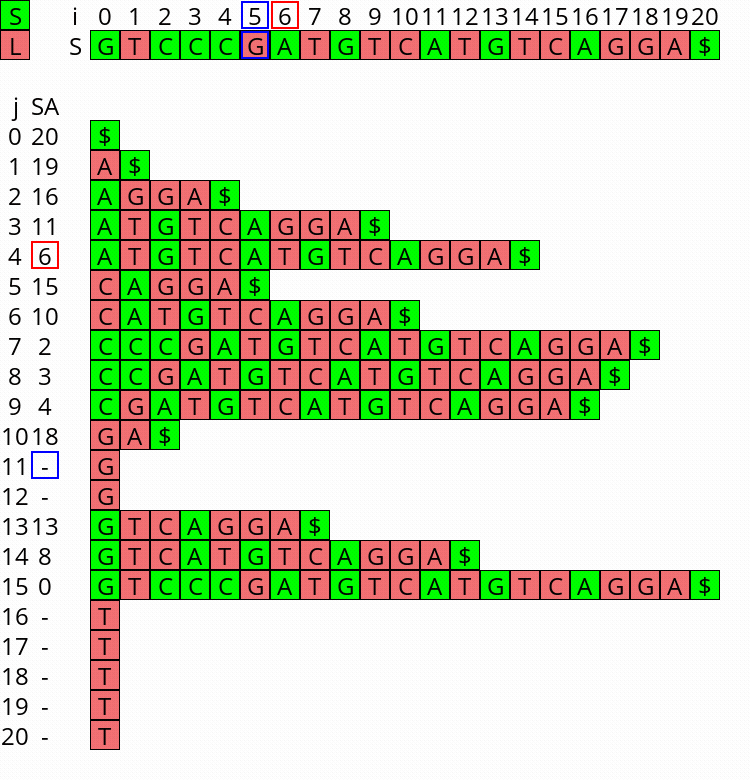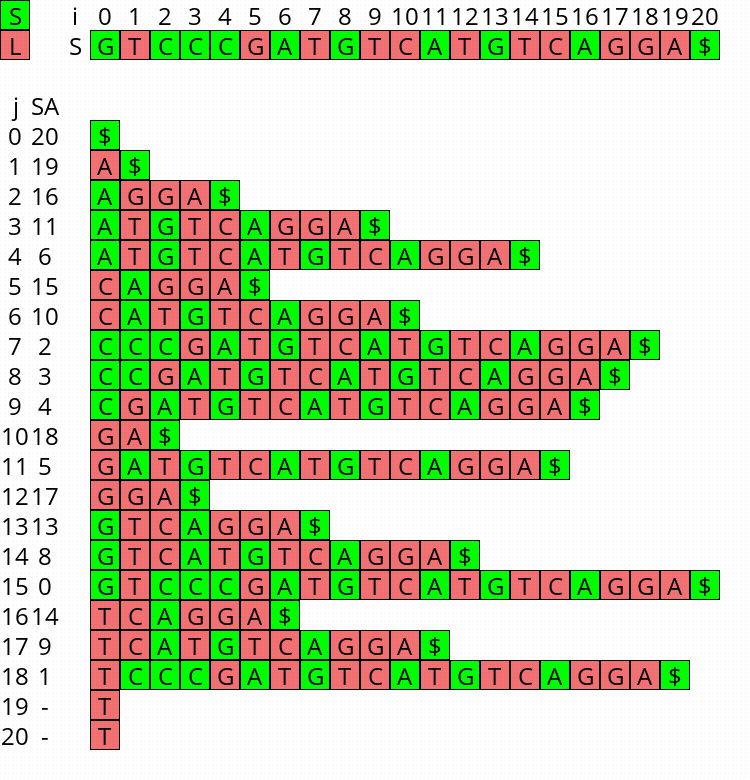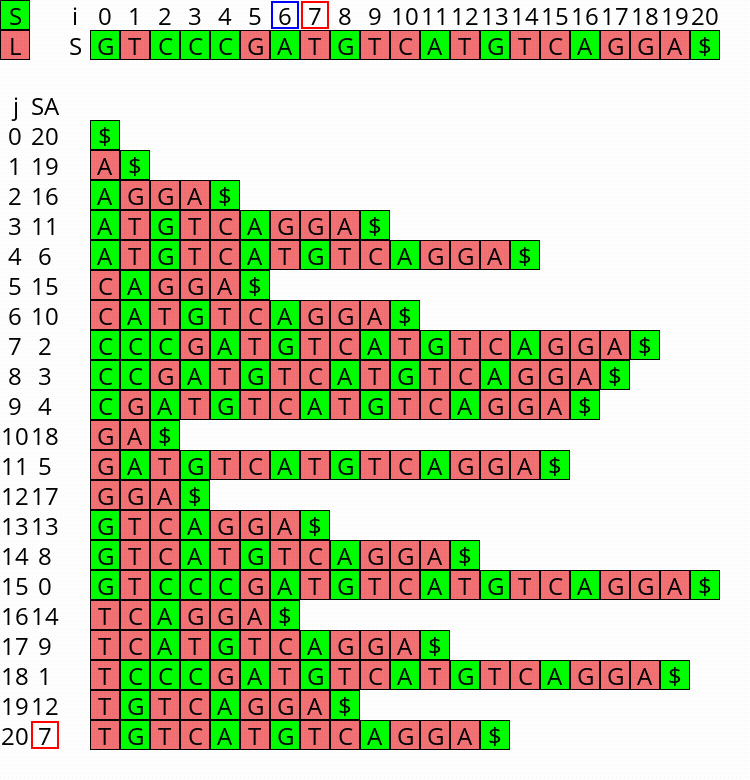
Figure 1: Constructing the complete suffix array starting after step 2 above, with the small suffixes already filled at the ends of their buckets.
References Link to heading
Proof omitted. ↩︎