The complexity and performance of WFA and band doubling

November 2022 9-minute read

Table of Contents

Complexity analysis
Implementation efficiency
- Band doubling for affine scores was never implemented
WFA vs band doubling for affine costs
Conclusion
- Future work

This note explores the complexity and performance of band doubling (Edlib) and WFA under varying cost models.

Edlib (Šošić and Šikić 2017) uses band doubling and runs in $O(ns)$ time, for sequence length $n$ and edit distance $s$ between the two sequences.

WFA (Marco-Sola et al. 2020) uses the diagonal transition method and runs in expected $O(s^2+n)$ time.

Complexity analysis

Complexity of edit distance

Let’s go a little bit into how these complexities arise in the case of edit distance:

Edlib / band doubling: $O(ns)$: Let’s say the band doubling ends at cost $s\leq s’< 2s$. At that point, $2s’+1$ diagonals have been processed¹, and the total cost of trying all smaller $s’$ is an additional $2s’$ diagonals, for a total of $4s’+1 \leq 8s+1 = O(s)$ diagonals. Each diagonal contains $n$ (or slightly fewer) states, so that the overall complexity is $O(ns)$.
WFA / diagonal transition: $O(s^2+n)$: At the time WFA ends, it has visited exactly $2s+1$ diagonals. On each diagonal, there are up to $s+1$ farthest reaching states, one for each distance $1$ to $s$. This makes for a total of $O(s^2)$ f.r. states. Note that I’m ignoring the extended states here. Myers (1986) shows that that’s OK.

Complexity of affine cost alignment

Now, let’s think what happens when we change the cost model from edit distance to some affine cost scheme. This means that the alignment score $s$ will go up. Let $e$ be the least (in case of multiple affine layers) cost to extend a gap. Now, we get this analysis:

Edlib / band doubling: $O(ns/e)$: The number of diagonals visited changes to $2\cdot s/e+1$, since any diagonal more than $s/e$ away from the main diagonal has cost $>e\cdot s/e=s$ to reach. The number of states on each diagonal is still $n$, so the overall complexity is $O(ns/e)$.
WFA / diagonal transition: $O(s^2/e+n)$: Like with Edlib, the number of visited diagonals reduces to $s/e$. The number of furthest reaching states remains² $s$. Thus, the overall complexity is $O(s^2/e+n)$.

Comparison

Now let’s think what this means for the relative complexity of Edlib $O(ns/e)$ and WFA $O(s^2/e)$: it’s the difference between $n$ and $s$. This means that as soon as the alignment cost $s$ gets close to $n$, Edlib should start to outperform WFA. In practice, this should mean that WFA/diagonal transition is relatively better for unit costs and small affine costs, whereas edlib is better when affine costs are large. Or equivalently, the maximum error rate at which WFA is faster than edlib should go down as the affine penalties increase.

Implementation efficiency

WFA (WFA2-lib, that is) supports both edit distance and affine costs. Single layer affine costs has to compute $3$ instead of $1$ layers, so will be a bit slower.³

Edlib only implements edit distance. It does this extremely efficiently using Myers’ bit-vector algorithm. This allows for both bit-packing (storing multiple DP states in a single usize integer) and SIMD, which should give a $10\times$ to $100\times$ constant speedup.⁴ However, Edlib does not implement affine scoring, which bring me to:

Band doubling for affine scores was never implemented

I am not aware of any library that (competitively, or at all really) implements band doubling for affine costs. KSW2 implements banded alignment for affine costs efficiently using the differences method of Suzuki and Kasahara (2018), which could be seen as the equivalent of Myers’ bit-packing for affine scores.

However, as stated in the readme, KWS2 fails to implement band doubling. It seems that KSW2 is mostly used for heuristic alignment, where a band is chosen in other ways. This means that for exact alignment, it falls back to $O(n^2)$.

I did implement band doubling for affine costs as part of A*PA in a NW aligner that can handle arbitrary cost models, but for now this implementation is focused on the algorithm rather than efficiency, and it does not use any kind of SIMD and/or bit-packing.

WFA vs band doubling for affine costs

What we’ve learned so far:

WFA has better complexity when $s \ll n$.
Edlib has better complexity when $s \gg n$.
Edlib’s implementation is extremely efficient⁵, so let’s change that to $s\ll n/10$ or so.⁶
For affine costs, no efficient implementation of the $O(ns)$ band doubling method exists.

So now the question is, how would WFA compare to band doubling for affine scores? The WFA paper contains the following comparison. I’m interested in the synthetic data results for WFA, KSW2-Z2⁷, and Edlib.

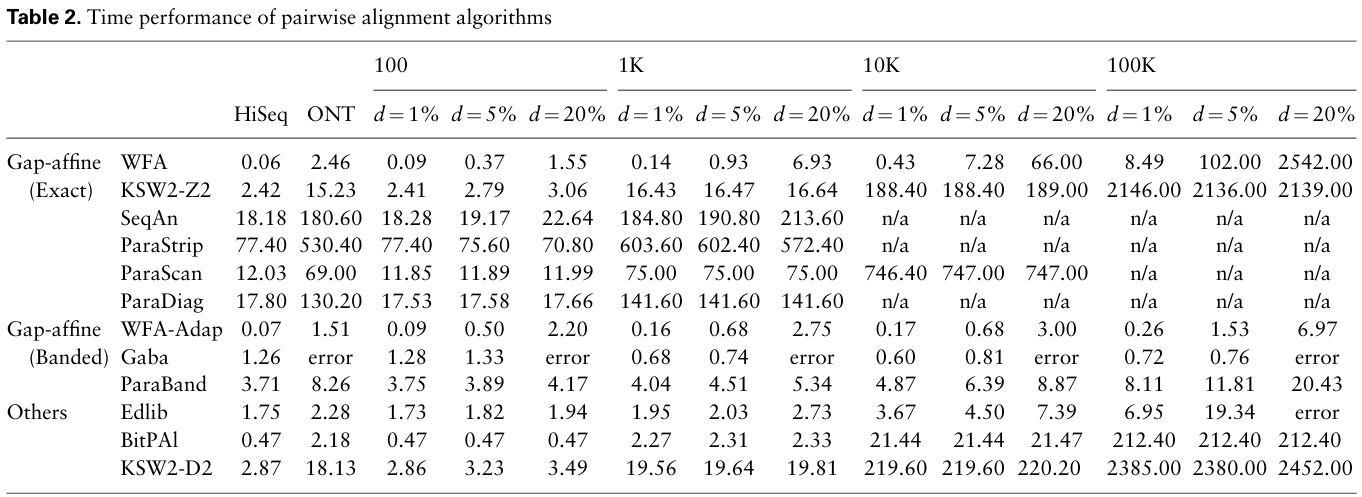
Figure 1: Table 2 from Marco-Sola et al. (2020) compares WFA performance to KWS2 and other aligners for affine costs with mismatch x=4, gap-open o=6 and gap-extend e=2. Errors are uniform. The bottom three aligners use edit distance, and the three above are approximate. For each n, the time shown is to align a total of 10M bp. — Figure 1: Table 2 from Marco-Sola et al. (2020) compares WFA performance to KWS2 and other aligners for affine costs with mismatch `x=4`, gap-open `o=6` and gap-extend `e=2`. Errors are uniform. The bottom three aligners use edit distance, and the three above are approximate. For each `n`, the time shown is to align a total of `10M` bp.

First some remarks about the numbers here:

Scaling with $d$

Edlib should scale as $O(ns) = O(nd)$. I have absolutely no clue why it’s only at most $2\times$ slower for $d=20\%$ compared to $d=1\%$ instead of $20\times$. Something feels off here. Maybe it’s only IO overhead that’s being measured? Or maybe Edlib uses an initial band that’s larger than the actual distance?
KWS2’s runtime is $O(n^2)$ and independent of $d$. I suppose the variation for small $n$ (2.4s vs 3.0s) is just measurement noise.⁸
For WFA, for $n=100k$ the scaling indeed seems to be roughly $d^2$, with $d=20\%$ being $300$ (instead of $400$) times slower than $d=1\%$. For smaller $n$, the scaling seems to be less. For small $n$ and/or $d=1\%$ this is probably because of the constant $+n$ overhead on top of the $s^2$ term.

Scaling with $n$

Given Edlib’s $O(ns)$ runtime, we expect it to become $10\times$ slower per basepair when $n$ goes times $10$.⁹ In practice, the only significant jump is from $10K$ to $100K$, but even that is only a factor $5$ at most. Again this hints at some constant/linear overhead being measured, instead of the quadratic component of the algorithm itself.
Like Edlib, KSW2’s runtime per basepair should go $\times 10$ when $n$ goes $\times 10$. This indeed seems to be the case, within a ${\sim}20\%$ margin.
Again, we expect WFA’s runtime per basepair to scale with $n$. For $n\geq 10k$, this indeed seems to be roughly the case.

So now we can ask ourselves: how much would KSW2 improve if it supported band doubling? The complexity goes from $O(n^2)$ to $O(ns/e)$. For now let’s say $e$ is constant.¹⁰ So we should get a $O(n/s)=O(1/d)$ speedup, where $d$ is the relative error rate. If we look at the table and divide each value in the KSW2 row by $1/d\in \{100, 20, 5\}$, WFA is still faster than KSW2 in some cases, but never by more much!

Table 1: Scaled KSW2 results, manually scaled down from O(n^2) to O(ns) by multiplying runtimes by $d$.

	n	100	100	100	1K	1K	1K	10K	10K	10K	100K	100K	100K
alg	d (%)	1	5	20	1	5	20	1	5	20	1	5	20
WFA		0.09	0.37	1.55	0.14	0.93	6.93	0.43	7.28	66.00	8.49	102.00	2542.00
KSW2$\cdot d$		0.024	0.14	0.61	0.164	0.82	3.32	1.88	9.42	37.8	21.4	106.8	427.8

After scaling, we can see that if KSW2 supported band doubling, it might be faster than WFA for many inputs and only slightly slower on those where it’s not, in particular at $1\%$ low error rates.

Of course I have ignored constants here: This is assuming that $s/e$ roughly equals the error rate¹¹, and omitting the fact that band doubling can be up to $2$ times slower than simply computing the states within the optimal band.

Conclusion

Clearly the WFA implementation is much better than any other affine-cost aligner out there, but the benefit of diagonal transition over an efficient (bit-packed, SIMD) band doubling implementation is not so clear-cut to me. At $1\%$ error rates WFA may indeed be faster, but for error rate $5\%$ and up this may not be true. The WFA paper shows over $100\times$ speedup compared to KSW2, but may only show a small constant speedup compared to band doubling.

For unit-costs alignments, the evaluations for A*PA (Groot Koerkamp and Ivanov 2024) show that WFA is up to $100\times$ faster than edlib for $d=1\%$.

Also note that these numbers are with relatively low affine costs. As they increase, I expect the benefit of WFA to get smaller.

Future work

Really, somebody¹² should patch KSW2 to support band doubling and rerun the WFA vs KSW2 vs Edlib comparison. I’d be curious to see results!

Also, it would be nice to have some analysis on how affine alignment score scales with cost model paremeters.

References

Groot Koerkamp, Ragnar, and Pesho Ivanov. 2024. “Exact Global Alignment Using A* with Chaining Seed Heuristic and Match Pruning.” Edited by Tobias Marschall. Bioinformatics 40 (3). https://doi.org/10.1093/bioinformatics/btae032.

Marco-Sola, Santiago, Juan Carlos Moure, Miquel Moreto, and Antonio Espinosa. 2020. “Fast gap-affine pairwise alignment using the wavefront algorithm.” Bioinformatics 37 (4): 456–63. https://doi.org/10.1093/bioinformatics/btaa777.

Myers, Gene. 1986. “An $O(ND)$ Difference Algorithm and Its Variations.” Algorithmica 1 (1–4): 251–66. https://doi.org/10.1007/bf01840446.

Suzuki, Hajime, and Masahiro Kasahara. 2018. “Introducing Difference Recurrence Relations for Faster Semi-Global Alignment of Long Sequences.” BMC Bioinformatics 19 (S1). https://doi.org/10.1186/s12859-018-2014-8.

Šošić, Martin, and Mile Šikić. 2017. “Edlib: A c/c++ Library for Fast, Exact Sequence Alignment Using Edit Distance.” Edited by John Hancock. Bioinformatics 33 (9): 1394–95. https://doi.org/10.1093/bioinformatics/btw753.

This can easily be reduced by a factor two by using the gap-cost heuristic and only visiting states on diagonals at distance at most s/2, but that doesn’t change the overall picture. ↩︎
assuming costs are coprime ↩︎
In fact, Santiago told me that in both cases the bottleneck tends to be the extension step, making them roughly as fast. Adding a second affine layer will slow things down though. ↩︎
I wish I had an exact number. ↩︎
WFA is super efficient too. But Edlib is just ridiculous! ↩︎
This really needs some numbers. But this is just a quick blog post. ↩︎
Z2 is the variant with one affine layer; D2 has two affine layers. ↩︎
Don’t put more decimals than you have accuracy. ↩︎
Remember, the table shows the total time to align $10M$ basepairs. ↩︎
I know; I wrote half this post about $e$, but for this part the cost model and extension cost $e=2$ are fixed anyway. ↩︎
This should be a relatively quick experiment to confirm. ↩︎
Future me? ↩︎