PtrHash

July 2025 4-minute read

Ragnar {Groot Koerkamp}

slides mphf

Minimal Perfect Hash Functions Link to heading

A set of \(n\) keys Link to heading

A hash function Link to heading

A hash function: collisions! Link to heading

A hash function: injective / perfect Link to heading

A hash function: bijective / minimal & perfect Link to heading

Problem statement Link to heading

Given a set of \(n\) keys \(K\subseteq \mathbb K\), build a function \(h\) satisfying

\(h(K) = \{0, \dots, n-1\}\): \(h\) is minimal & perfect.

Why? Array of \(n\) values as space-efficient value store.

Solutions take \(\log_2(e) {=} 1.443\) to \(3\) bits/key.

Goals of PtrHash:

at most 3 bits/key (you probably store ≥16 bit values anyway),
fast to evaluate,
fast to construct.

Previous & parallel work Link to heading

FCH: Fox, Chen, and Heath (1992)
CHD: Belazzougui, Botelho, and Dietzfelbinger (2009)

PTHash: Pibiri and Trani (2021)
PHOBIC: Hermann et al. (2024)

PHast: Beling and Sanders (2025)
Consensus: Lehmann, Sanders, et al. (2025)
Survey: Lehmann, Mueller, et al. (2025)

\[ \newcommand{\lo}{\mathsf{lo}} \newcommand{\hi}{\mathsf{hi}} \]

Naive: try seeded hashes Link to heading

Naive: \(n^n / n!\approx e^n\) tries, \(n\cdot\log_2 e\) bits Link to heading

Construction Link to heading

Build \(h\) incrementally using buckets Link to heading

Build \(h\) incrementally Link to heading

Better: assign buckets from large to small Link to heading

Skew bucket sizes Link to heading

Remapping: avoiding the hard part Link to heading

Remapping: add \(1\%\) extra slots Link to heading

Remapping: map extra slots back Link to heading

Queries Link to heading

Query: 1. Hash key Link to heading

Query: 2. Lookup bucket Link to heading

Query: 3. Compute slot Link to heading

PTHash Link to heading

Iterate seed values (pilots) until a hit is found.
Dictionary compression to handle large values.

PtrHash Link to heading

Iterate seed values (pilots) until a hit is found.
Dictionary compression to handle large values.

“Inlined” 8-bit pilots for fast lookup
Handle impossible buckets by evicting others
- When none of the \(2^8=256\) seeds are collision free, choose the one with minimal number of collisions, and break ties towards evicting small buckets.
- Eviction: “unassign” a seed, and put the bucket back in the queue.
- Distributes the entropy from the hard buckets over all seeds.

\(\varepsilon\) cost sharding Link to heading

\(S\) shards
PTHash, PHOBIC: shards of expected size \(a = n/S\), real size \(a_i\)
- \(a / \lambda\) buckets per shard, \(a_i/\alpha\) slots per shard
- Store shard offsets
PtrHash: \(a / \lambda\) buckets per shard, \(a /\alpha\) slots per shard
- Direct indexing
Shard size follows from Sebastiano’s formula

PtrHash with array vs VFUNC Link to heading

VFUNC, storing \(b\) bit values:
- 10% memory overhead: \(b n + 0.1 b n\)
- 3 independent/parallel reads
PtrHash:
- 3 bits overhead: \(b n + 3n\)
- 2 dependent/sequential reads

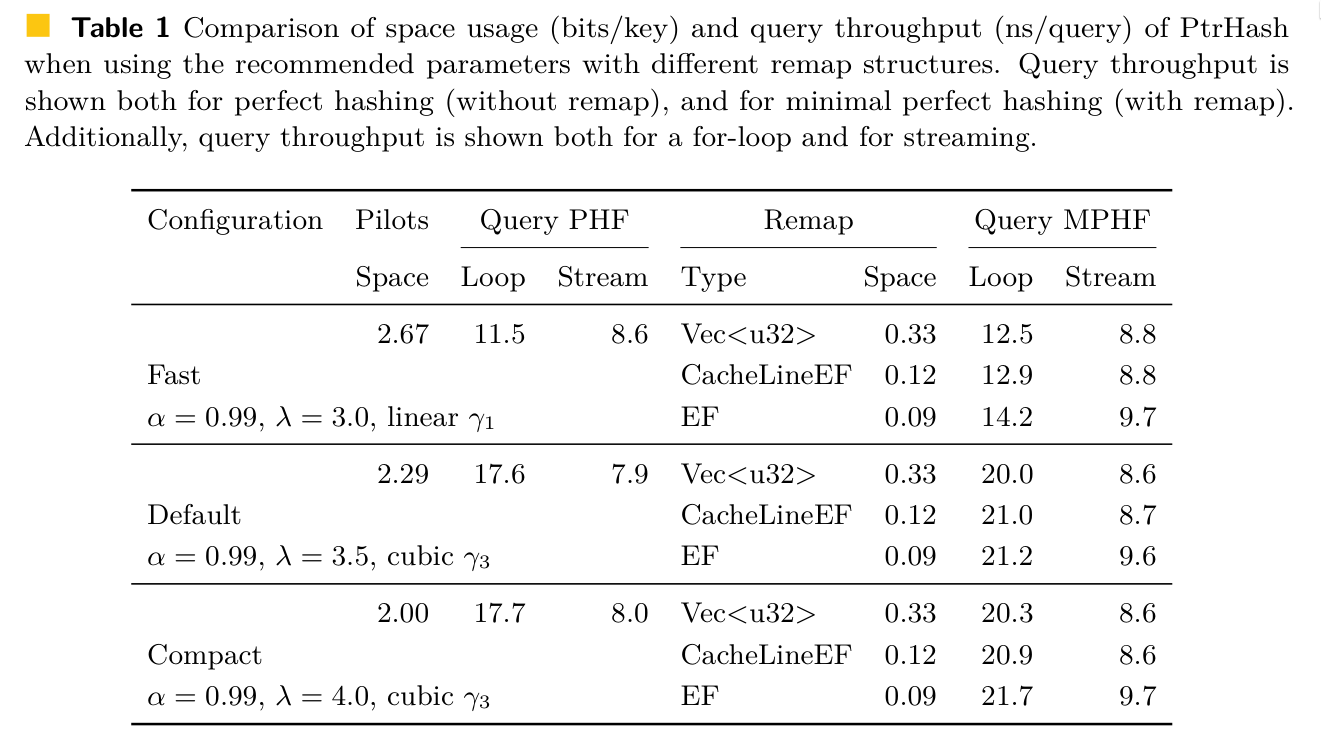
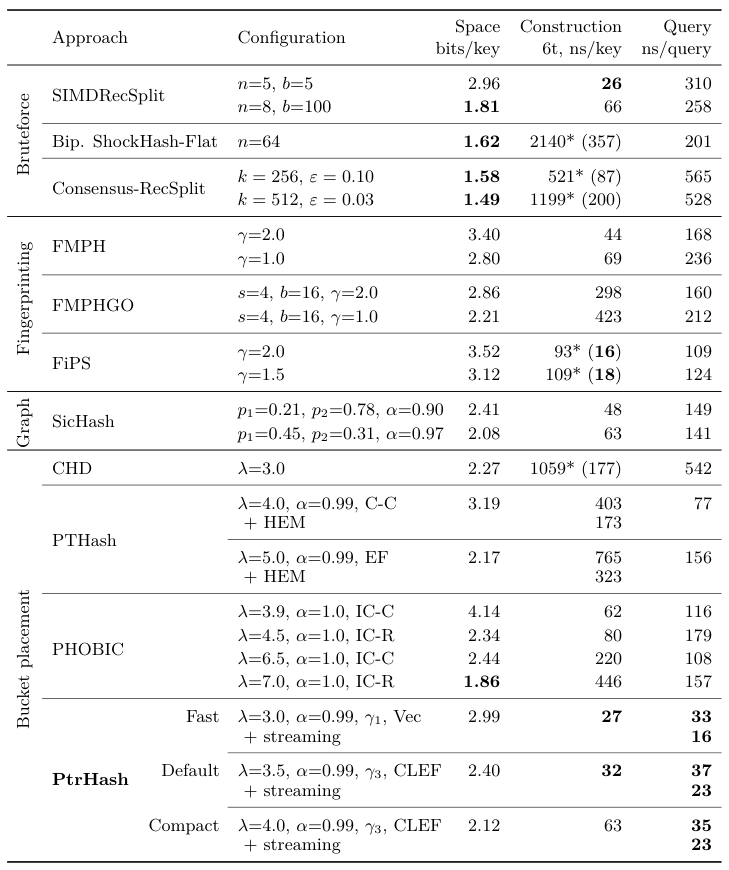
Results Link to heading

Construction time vs. size Link to heading

Comparison Link to heading

300M variable length string keys

<3 bits/key
fastest queries by 2x to 4x
also fast construction

Queries: looping, batching, streaming Link to heading

A simple loop Link to heading

Setup: PtrHash on \(10^9\) integer keys; 300 MB.
Fact: Most queries need uncached data from RAM.
Fact: Reading RAM takes 80 ns
Question: how long does this take? (>90, ≈80, 40-60, <30)

1
2
3
for k in keys {
    h.query(k);
}

Answer: 12 ns!
- The CPU works on 7 iterations in parallel!
To measure latency:

1
2
3
4
let mut seed = 0;
for k in keys {
    seed ^= h.query(seed ^ k);
}

Batching & Streaming Link to heading

Batching:

1
2
3
4
5
6
7
8
for batch in keys.array_chunks::<32>() {
    for k in batch {
        h.prefetch_seed(k);
    }
    for k in batch {
        h.query(k);
    }
}

Streaming:

1
2
3
4
for i in 0..n {
    h.prefetch_seed(keys[i+32]);
    h.query(keys[i]);
}

Batching with Prefetching Link to heading

Batching & Prefetching Link to heading

Multithreading Link to heading

Conclusions Link to heading

Simple \(\implies\) fast
Partition data into cache-sized chunks
Streaming & prefetching for max throughput

Brought to you by Link to heading

Bonus slides Link to heading

Simple operations Link to heading

Hashing via \[h(x) = \lo(C\cdot x) = (C\cdot x)\mod 2^{64}.\]
Quadratic bucket function \[\gamma(x) = \hi(x\cdot x) = \lfloor x^2/2^{64}\rfloor.\]
Use fastmod for \(\mod n\)

Overview Link to heading

Parameters Link to heading