Optimal Throughput Bioinformatics

PhD Defense

Ragnar {Groot Koerkamp}

April 10, 2025

What is bio​informatics?

For today: DNA

Zephyris, CC BY-SA 3.0 Wikipedia

Also DNA

Human chromosomes

DNA, according to me

A C G T

00 01 10 11

Covid

A virus: SARS-CoV-2, aka COVID-19

Why bio​informatics?

1970-2000: Floppy disks - MB - Bacteria

Floppy

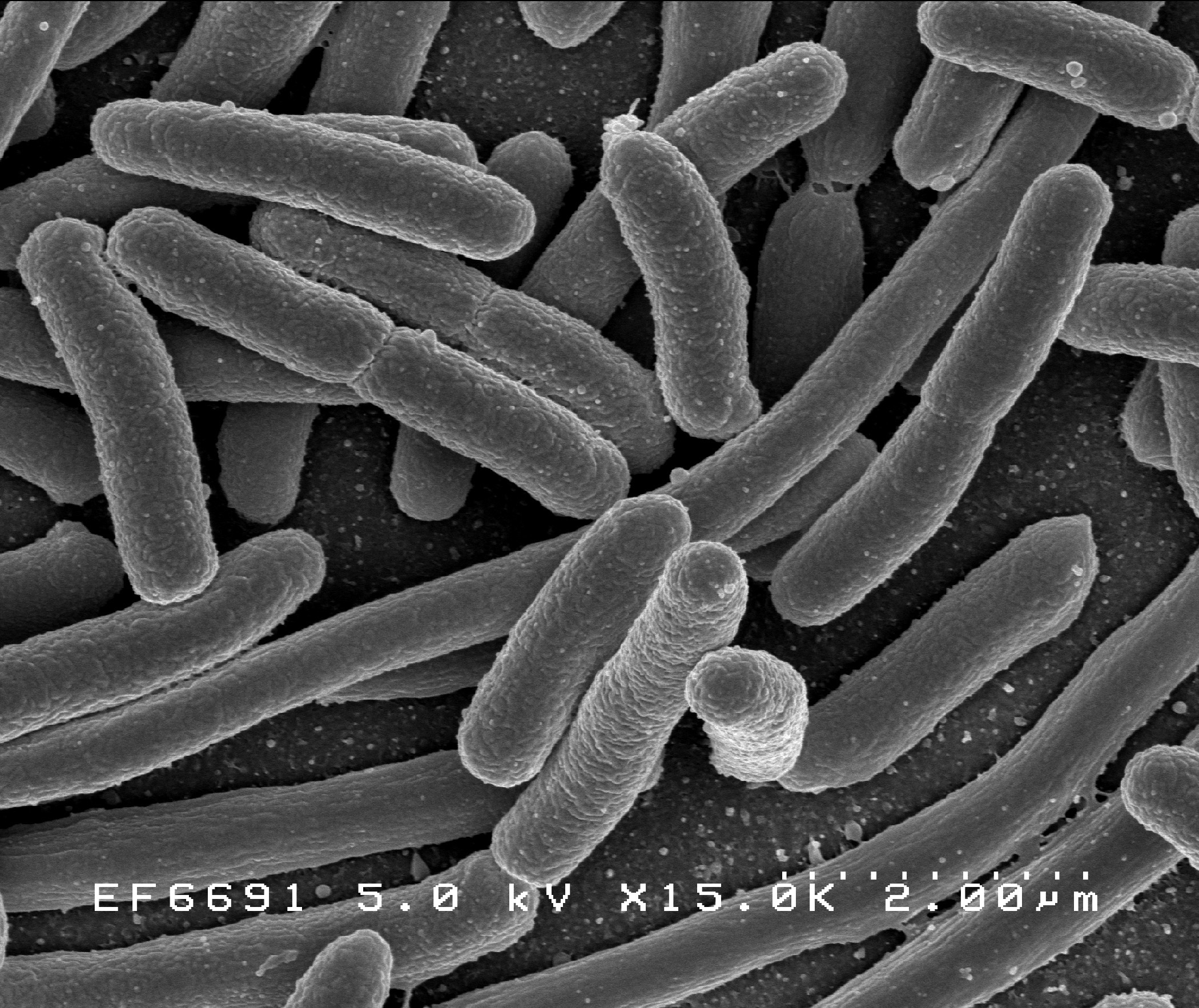
E. coli bacteria (1997)

2000-2020: USB stick - GB - Human Genome

USB stick

Human genome (2001)

2010-2020: Hard Drive - TB - RefSeq

Hard drive

RefSeq

2025: Data Center - PB - SRA

Data Center
PhonlamaiPhoto | istockphoto.com

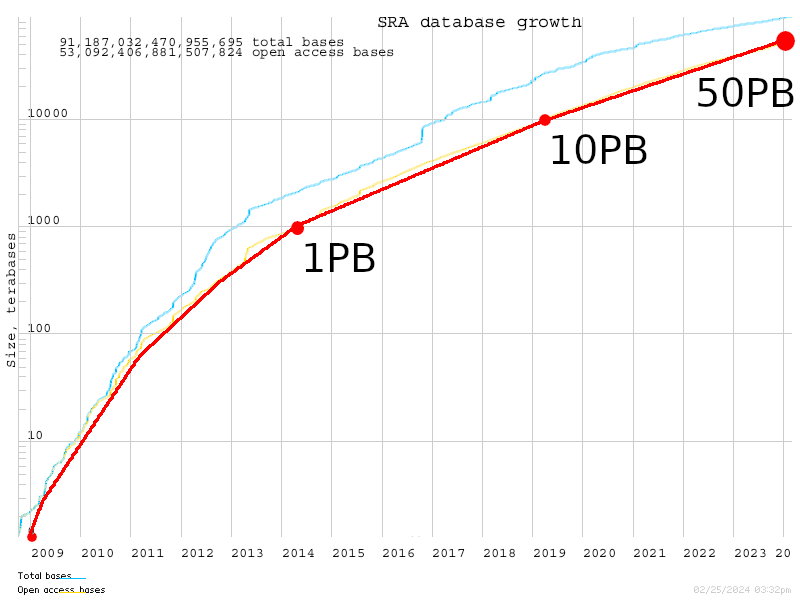
Growth of SRA

Goal:
Fast code

Goal:
High throughput code

Goal:
Optimal throughput code

What is high troughput code?

1. Complexity

   • Few operations:

     \(\quad O(n^2)\quad\longleftrightarrow\quad O(n)\)

2. Efficiency

   • Fast operations:

     memory read, 100 ns \(\quad\longleftrightarrow\quad\) 0.1 ns, addition

3. Implementation

   • Parallel operations:

     SIMD, instruction-level parallelism

Papers

Part 1: Pairwise Alignment

Part 2: Minimizers

Part 3: Optimal Throughput

Additional

• [1] A*PA: Exact Global Alignment Using A* with Chaining Seed Heuristic and Match Pruning.
  RGK and Pesho Ivanov, Bioinformatics 2024.
• [2] A*PA2: Up to 19x Faster Exact Global Alignment.
  RGK. WABI 2024.

• [3] The Mod-Minimizer: A Simple and Efficient Sampling Algorithm for Long k-mers.
  RGK and Giulio Ermanno Pibiri. WABI 2024.
• [4] Forward Sampling Scheme Density Lower Bound.
  Bryce Kille, RGK, et al. Bioinformatics 2024.
• [5] The Open-Closed Mod-Minimizer Algorithm.
  RGK, Daniel Liu, and Giulio Ermanno Pibiri. AMB 2025.

• [6] SimdMinimizers: Computing Random Minimizers, Fast.
  RGK and Igor Martayan. SEA 2025.
• [7] PtrHash: Minimal Perfect Hashing at RAM Throughput.
  RGK. SEA 2025.

• [8] U-index: A Universal Indexing Framework for Matching Long Patterns.
  Lorraine Ayad, Gabriele Fici, RGK, Rob Patro, Giulio Ermanno Pibiri, and Solon Pissis. SEA 2025.

Problem 1: Pairwise Alignment

Covid – \(\alpha\), December 2020

Sars-CoV-2, alpha variant, December 2020

Covid – \(\omicron\), December 2021

Sars-CoV-2, omicron variant, December 2021

Pairwise alignment

• Find the mutations between two sequences

Dynamic programming

Dynamic programming

Dynamic programming

Dynamic programming

Dynamic programming

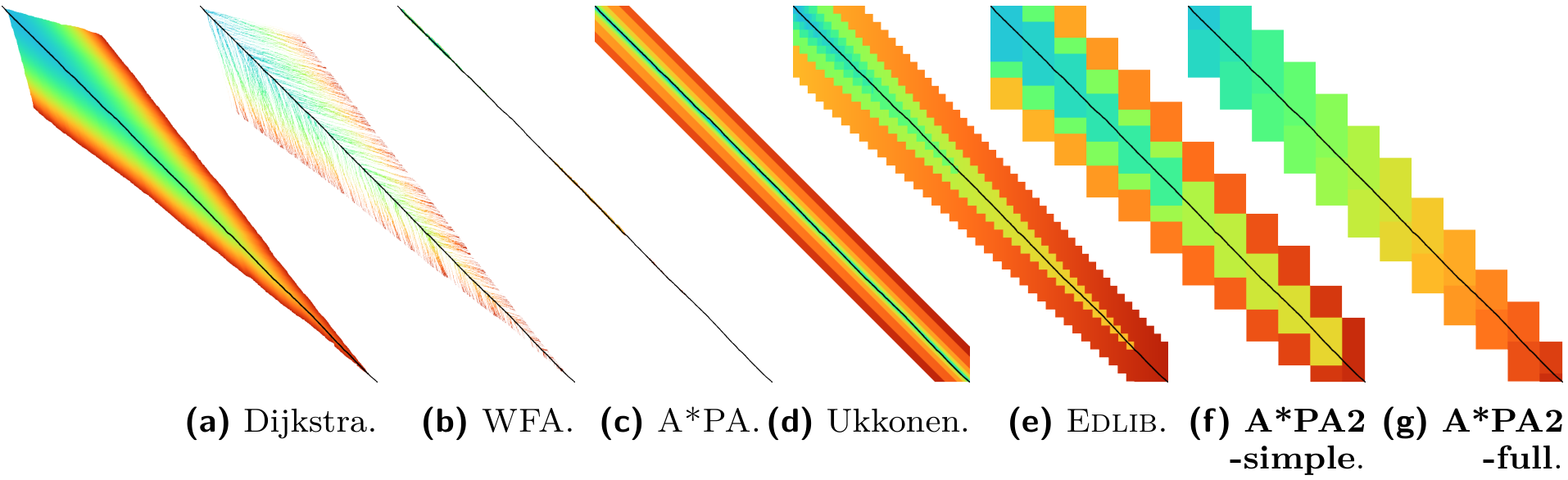
Needleman-Wunsch – Quadratic \(O(n^2)\)

Dijkstra – \(O(ns)\)

Diagonal transition – \(O(n + s^2)\)

A*PA\({}^{1}\) – near-linear, \(3\times\) faster on similar seqs

[1] Exact Global Alignment Using A* with Chaining Seed Heuristic and Match Pruning.
RGK and Pesho Ivanov, Bioinformatics 2024.

A*PA\({}^{1}\) – not quite linear

[1] Exact Global Alignment Using A* with Chaining Seed Heuristic and Match Pruning.
RGK and Pesho Ivanov, Bioinformatics 2024.

A*PA: Great complexity – terrible efficiency

Band Doubling – \(O(ns)\)

A*PA2\({}^{2}\) – good efficiency: up to \(19\times\) faster

[2] A*PA2: Up to 19x Faster Exact Global Alignment.
RGK. WABI 2024.

Problem 2: Minimizers – lossy compression

Lossy compression

original

Lossy compression

50%

Lossy compression

25%

Lossy compression

12%

Lossy compression

6%

Sampling k-mers

\(k=10\), \(w=1000\)

Minimizer definition

\(k\)-mer size: \(k=3\)
Window guarantee: \(w=4\)
Length \(w+k-1=6\) window of \(w\) \(k\)-mers

Minimizer scheme: \[ f: \Sigma^{w+k-1} \mapsto \{0, 1, 2, \dots, w-1\}. \]
Used for compression and hashing.

Minimizer example

Minimizer example

Minimizer example

Minimizer example

Minimizer example

Minimizer example

Minimizer density

Density: expected fraction of sampled \(k\)-mers.
Here: \(3/9=0.33\)

Sampling k-mers

\(k=10\), \(w=500\)

Sampling k-mers

\(k=10\), \(w=250\)

Sampling k-mers

\(k=10\), \(w=100\)

Sampling k-mers

\(k=10\), \(w=50\)

Sampling k-mers

\(k=10\), \(w=25\)

Sampling k-mers

\(k=10\), \(w=100\)

Sampling k-mers

\(k=11\), \(w=100\)

Sampling k-mers

\(k=12\), \(w=100\)

Sampling k-mers

\(k=20\), \(w=100\)

Sampling k-mers

\(k=30\), \(w=100\)

Goal: Minimize the number of sampled \(k\)-mers

Density plots – before (\(w=24\))

The Mod-Minimizer\({}^{3}\)

[3] The Mod-Minimizer: A Simple and Efficient Sampling Algorithm for Long k-mers. RGK and Giulio Ermanno Pibiri. WABI 2024.

A Near-Tight Lower Bound\({}^{4}\)

[4] Forward sampling scheme density lower bound. Bryce Kille, RGK, et al. Bioinformatics 2024.

Near-optimal schemes for small \(k\)

(Unpublished)

Extended mod-minimizer\({}^{5}\)

[5] The Open-closed mod-minimizer Algorithm. RGK, Daniel Liu, and Giulio Ermanno Pibiri. AMB 2025.

Proving The Lower Bound

• Suppose \(k=1\), and consider a cycle of \(w+1\) characters.
  Eg for \(w=4\):

  ABCDEABCDEABCDE

• Suppose we only sample 1 character:

  AB​C​DEAB​C​DEAB​C​DE

  The distance between samples is \(5 > w\)!

• Thus, we need at least two samples.
• Conclusion: the density is at least \(2/(w+1)\).

Conclusion: high troughput code matters!

1. Complexity

   • Few operations:

     A*PA: \(\quad O(n^2)\quad \mapsto\quad \ ``O(n)\text{''}\)

     Provably near-optimal minimizer schemes.

2. Efficiency

   • Fast operations:

     A*PA2 is up to 500x more efficient than A*PA; up to 19x faster than other methods.

3. Implementation

   • Parallel operations:

     A*PA2 uses SIMD and instruction-level parallelism.

Outlook

• Optimize all the code.
• Minimizers are not yet a fully solved problem.
• Proving optimality is hard.

Thanks!

Propositions

1. Complexity theory’s days are numbered.
2. \(\log \log n \leq 6\)
3. Succinct data structures are overrated.
4. There is beauty in mathematical perfection.
5. Too many PhDs are wasted shaving of small factors of complexities that will never be practical.
6. If a paper starts with “faster methods are needed”, it must talk about the implementation.
7. Fast code must exploit assumptions on the input.
8. Fast code puts requirements on the input format.
9. Optimizing ugly code is a waste of time.
10. Assembly is not scary.

Extra: Pairwise alignment

A*PA: comparison

A*PA heuristics

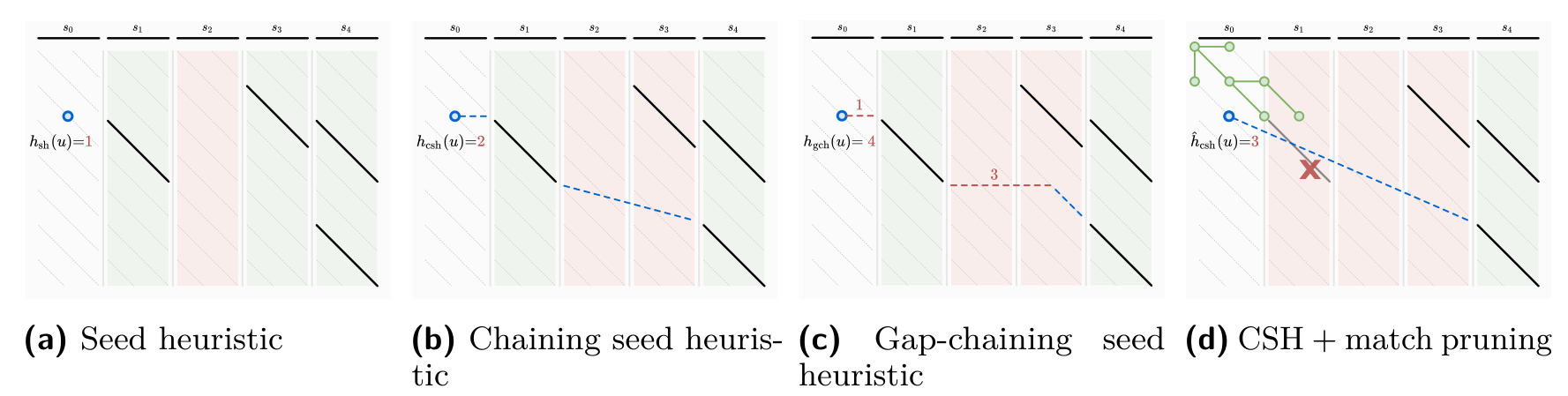
A*PA: seed heuristic

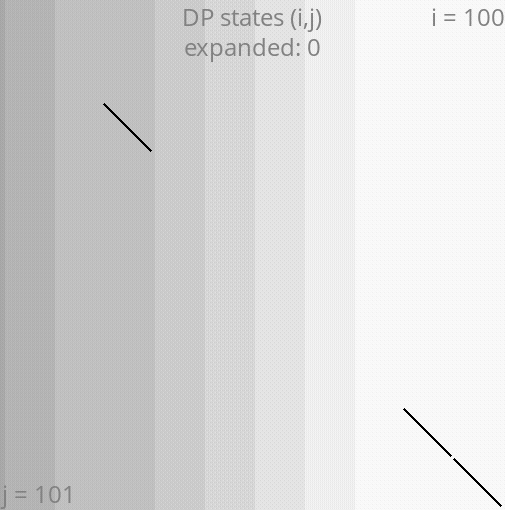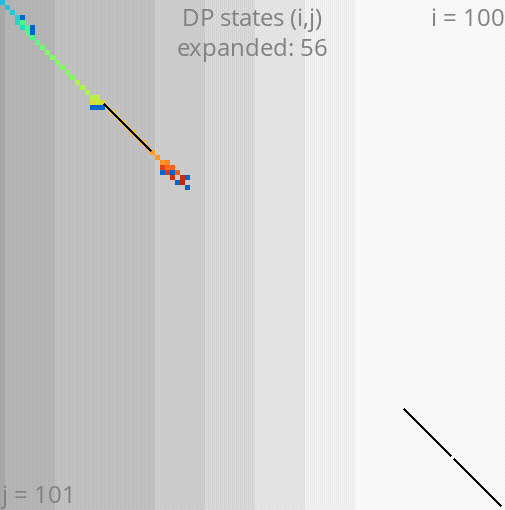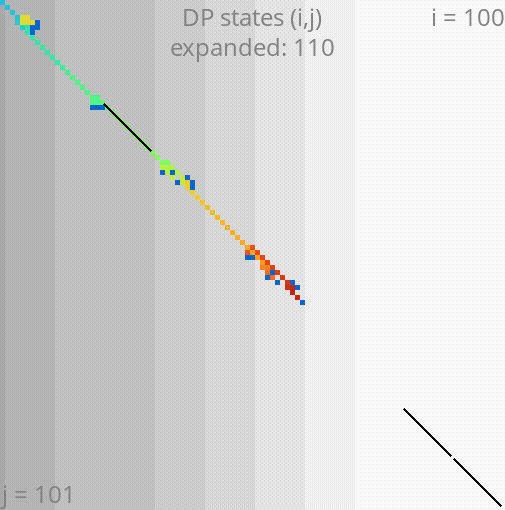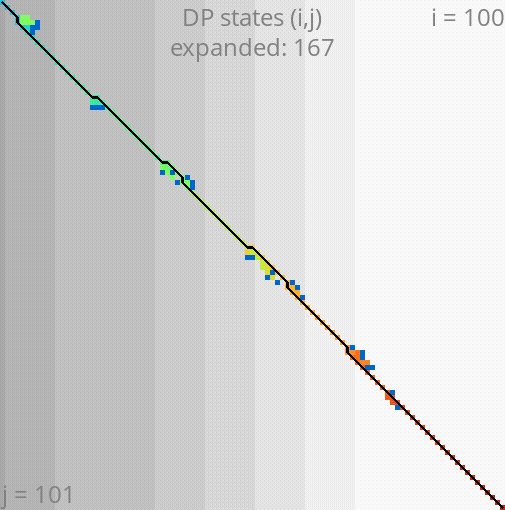
A*PA: gap-chaining seed heuristic

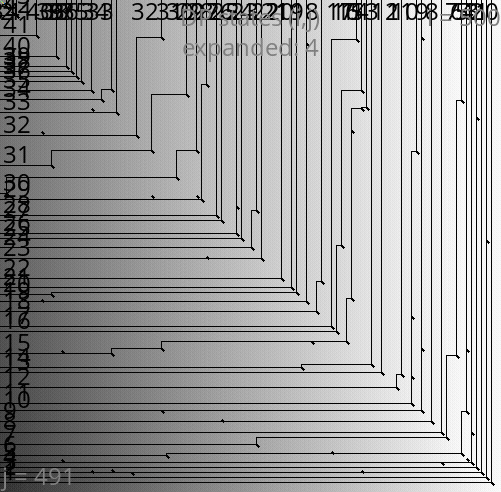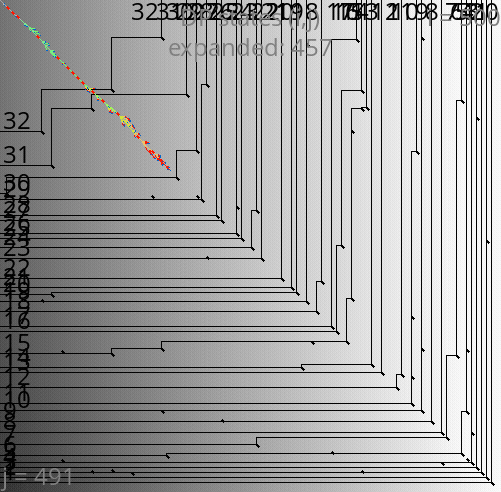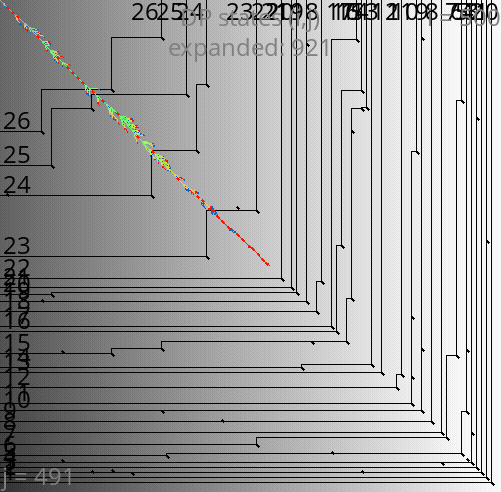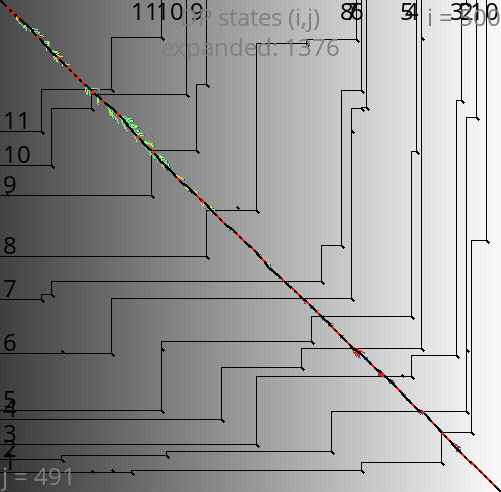
A*PA: contours

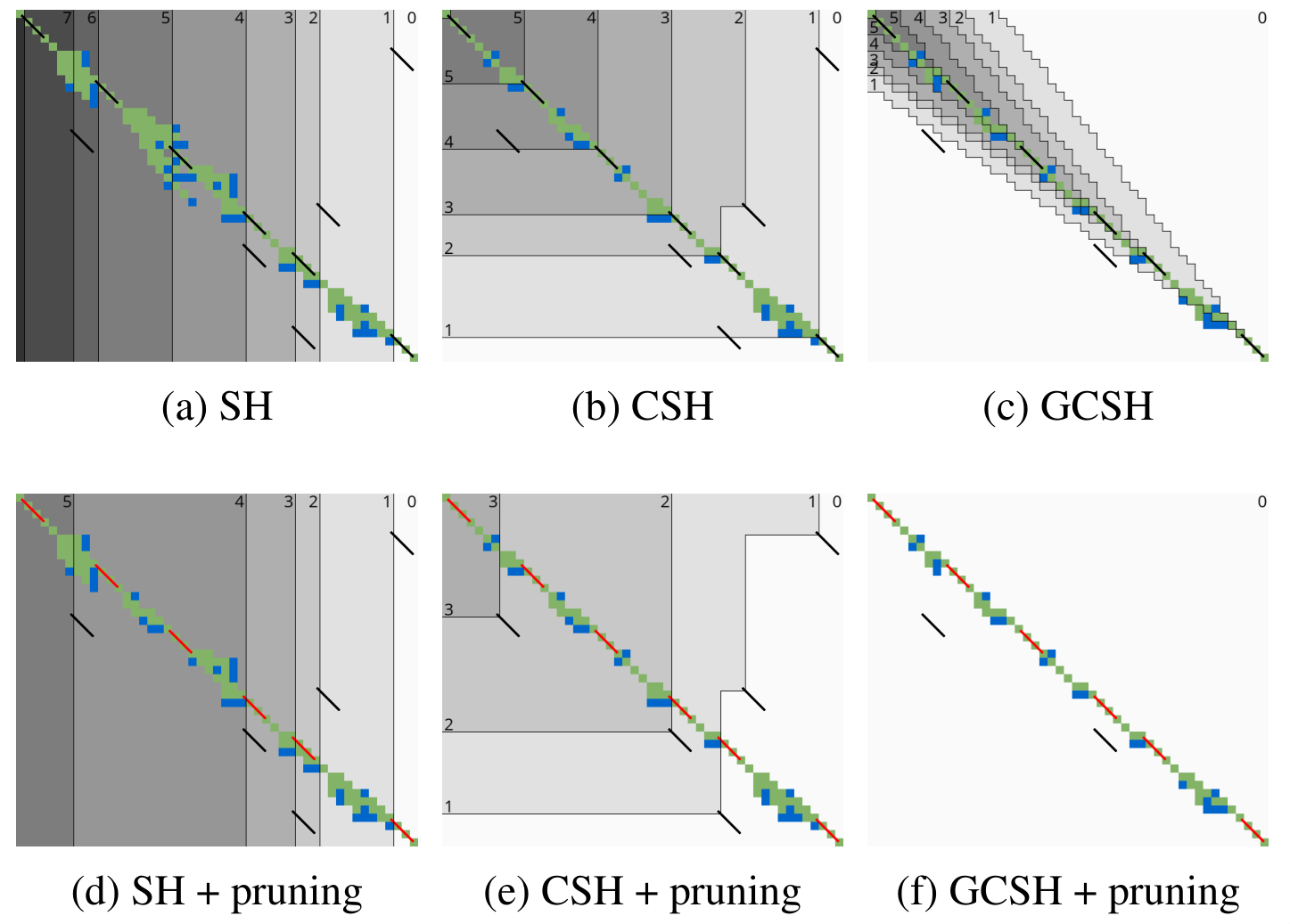
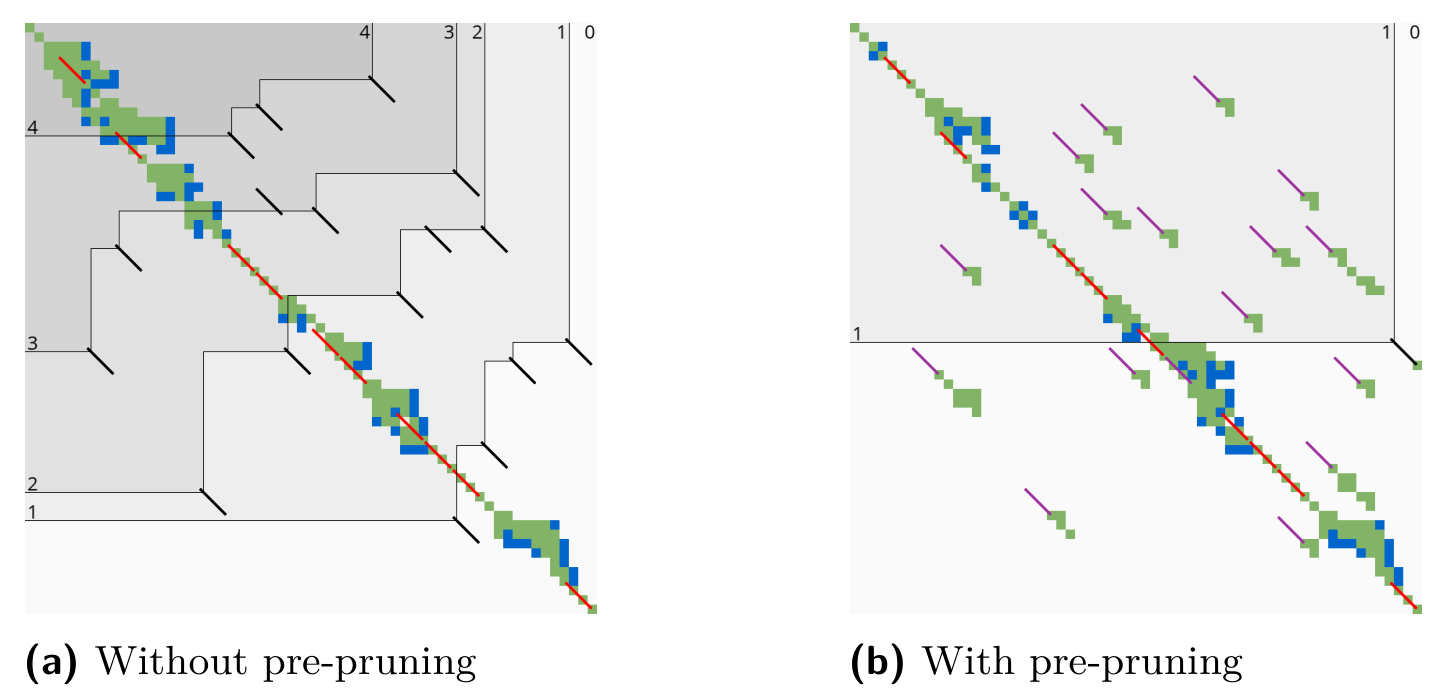
A*PA2: pre-pruning

A*PA2: results (real data)

A*PA2: results (synthetic)

Alignment modes

Cost models

Semi-global variants

Text searching

Skip-cost

Skip-cost

Block-computation results

Semi-global A*PA

Seed-chain-extend

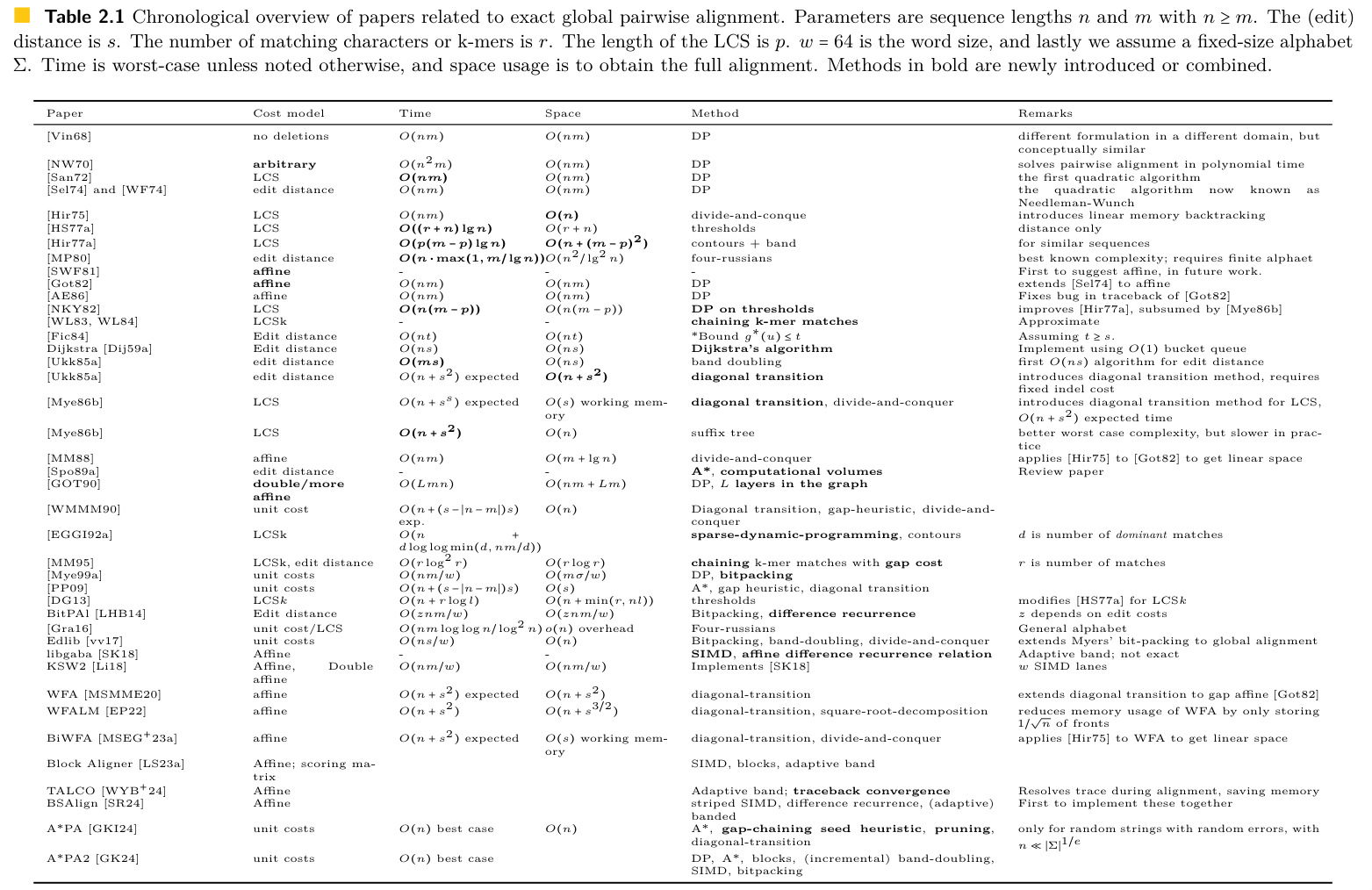
A*PA: table

Extra: Minimizers

Minimizer schemes

• Lexicographic: choose lexicographic smallest \(k\)-mer
• Random mini: choose \(k\)-mer with smallest hash
• ABB: choose A, followed by most non-A
• ABB+: break ties via random hash
• Sus-anchor: choose the position of the smallest unique suffix
  • “smallest”: where the first character is inverted.

Large alphabet

Lower bound

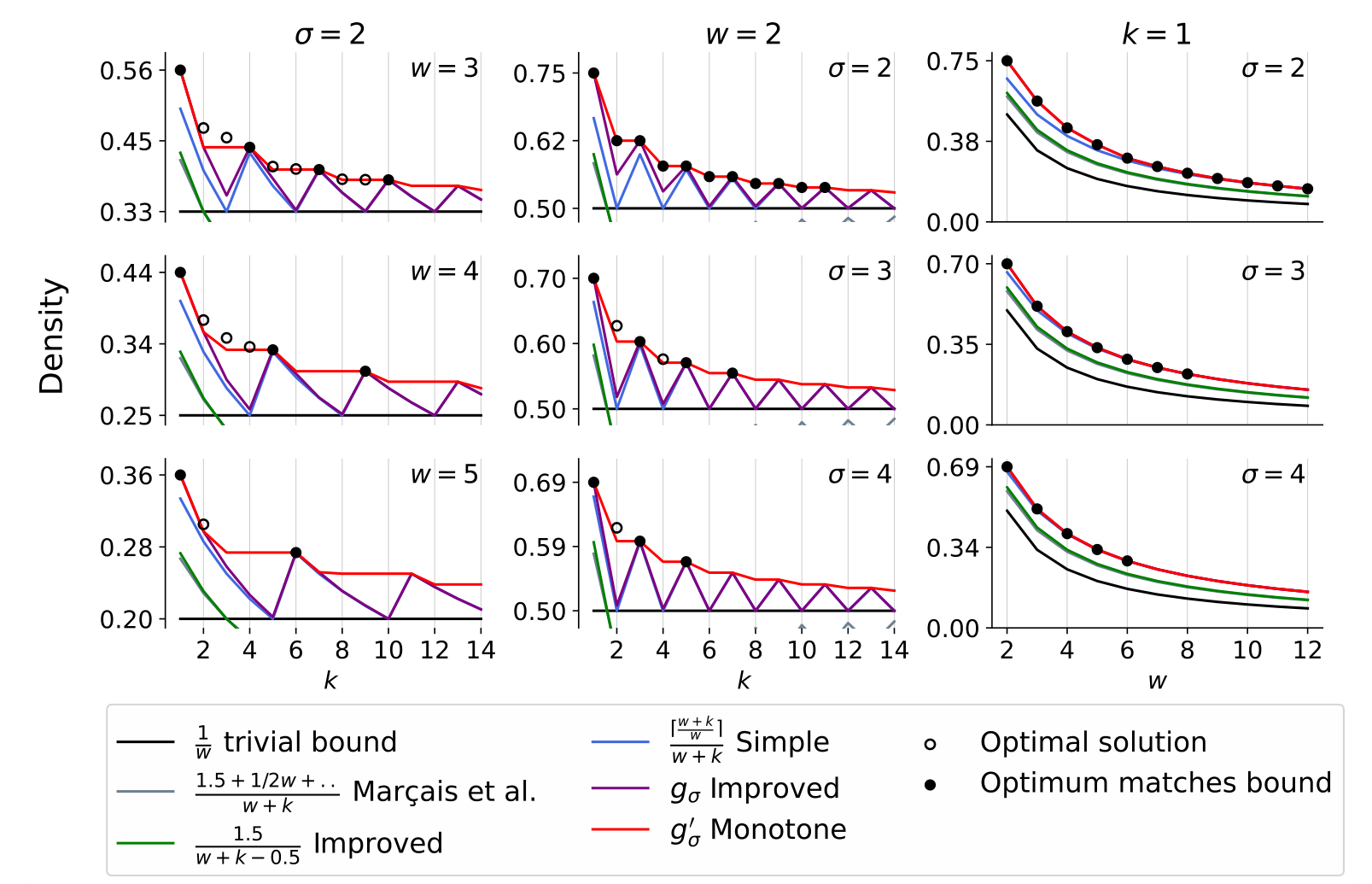
Mod-minimizer

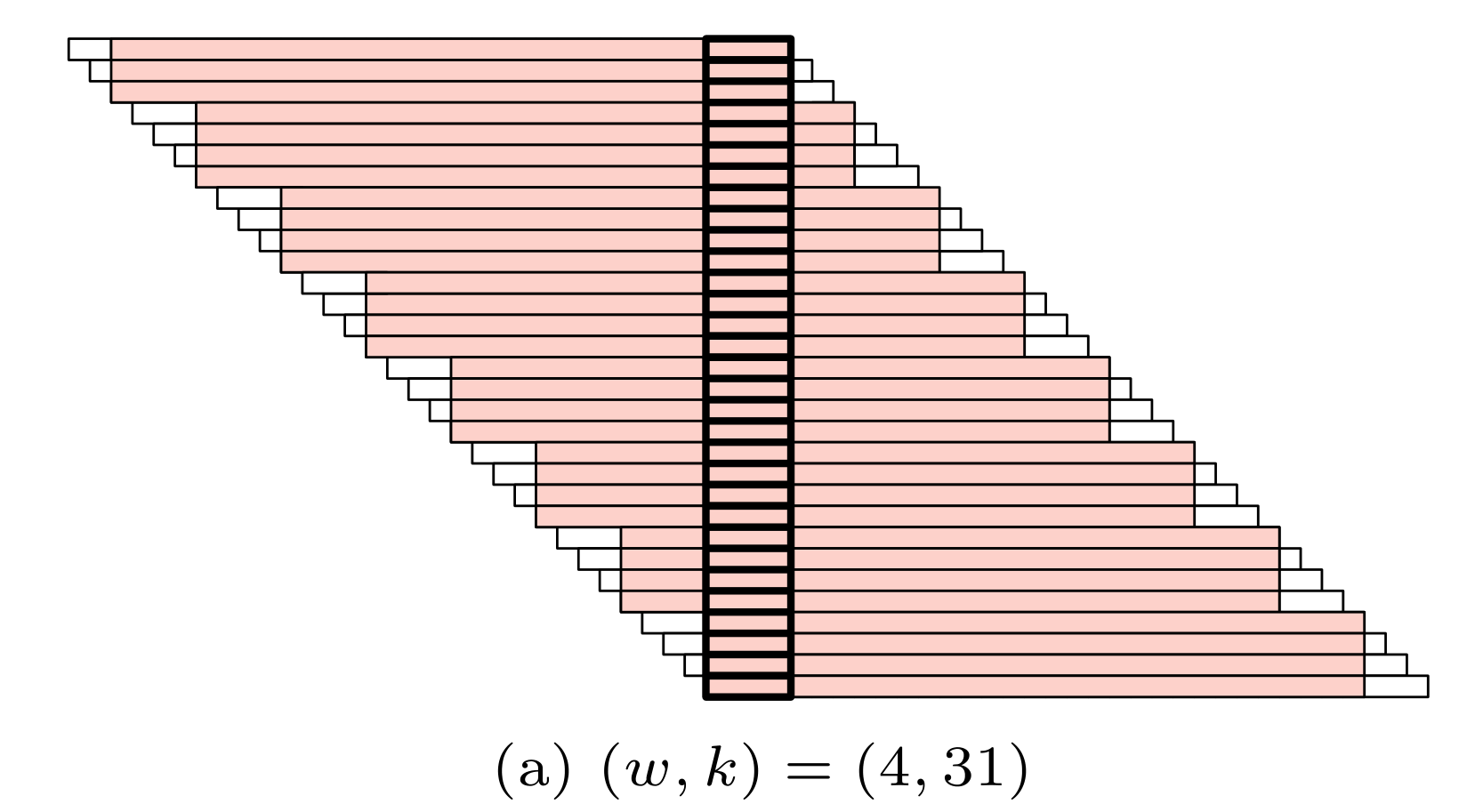
Mod-minimizer

Mod-minimizer

Mod-minimizer

Mod-minimizer

Mod-minimizer

Selection schemes

Extra: PtrHash

PtrHash: overview

PtrHash: Cacheline Elias Fano

PtrHash: Bucket Functions

PtrHash: Construction

PtrHash: Results

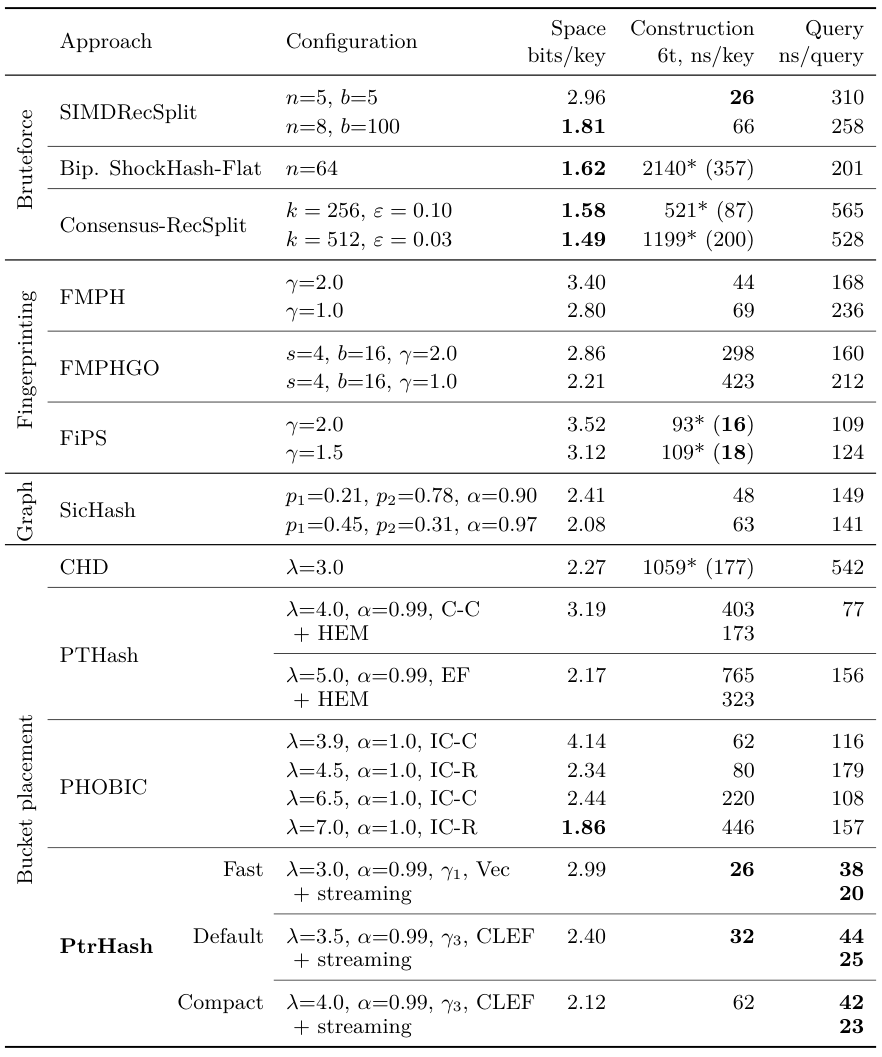
PtrHash: Optimal Throughput