Near-optimal sampling schemes

Ragnar Groot Koerkamp

2025-02-27 Thu 00:00

Created: 2025-04-23 Wed 15:27

1. Warming up: A cute prolblem

• Given a string, choose one character.
  • CABAACBD
• Given a rotation, choose one character.
  • ACBDCABA
• Can we always choose the same character?
• Yes: e.g. the smallest rotation (bd-anchor):
  • CAB​A​ACBD
  • ACBDCAB​A​

1.1. This talk: what if one character is hidden?

• Given a string (length \(w\)), choose one character.
  • CABAACBD​​X
• Given a rotation (of the hidden \(w+1\) string), choose one character.
  • ACBDXCAB​A
• Can we always choose the same character?
• Maybe?
  • CAB​A​ACBD
  • ACBDXCAB 🤔

1.2. The answer is no!

C​ABAACBDX rotations:

• C​AB​A​ACBD........
• .AB​A​ACBDX.......
• ..B​A​ACBDXC......
• ...​A​ACBDXCA.....
• ....ACBDXCAB.... <— the A is not here
• .....CBDXCAB​A​...
• ......BDXCAB​A​A..
• .......DXCAB​A​AC.
• ........XCAB​A​ACB

In the \(w+1\) rotations, we need at least 2 samples.

2. Minimizer schemes

\[\newcommand{\order}{\mathcal{O}}\]

• Minimizer scheme: Given a window of \(w\) k-mers, pick the (leftmost) smallest one
  • according to some order \(\order_k\)
• \(k=1\), \(w=5\):
  • C​A​BCA
• \(k=2\), \(w=5\):
  • C​AB​CAC.....
  • .​AB​CACC....
  • ..BC​AC​CX...
  • ...C​AC​CXY..
  • ....​AC​CXYZ.
  • .....​CC​XYZX
• Density: 3/10
  • C​AB​C​ACC​XYZX

2.1. The situation, 1 year ago

2.2. The mod-minimizer

2.3. A near-tight lower bound

2.4. The current picture

2.5. Greedymini

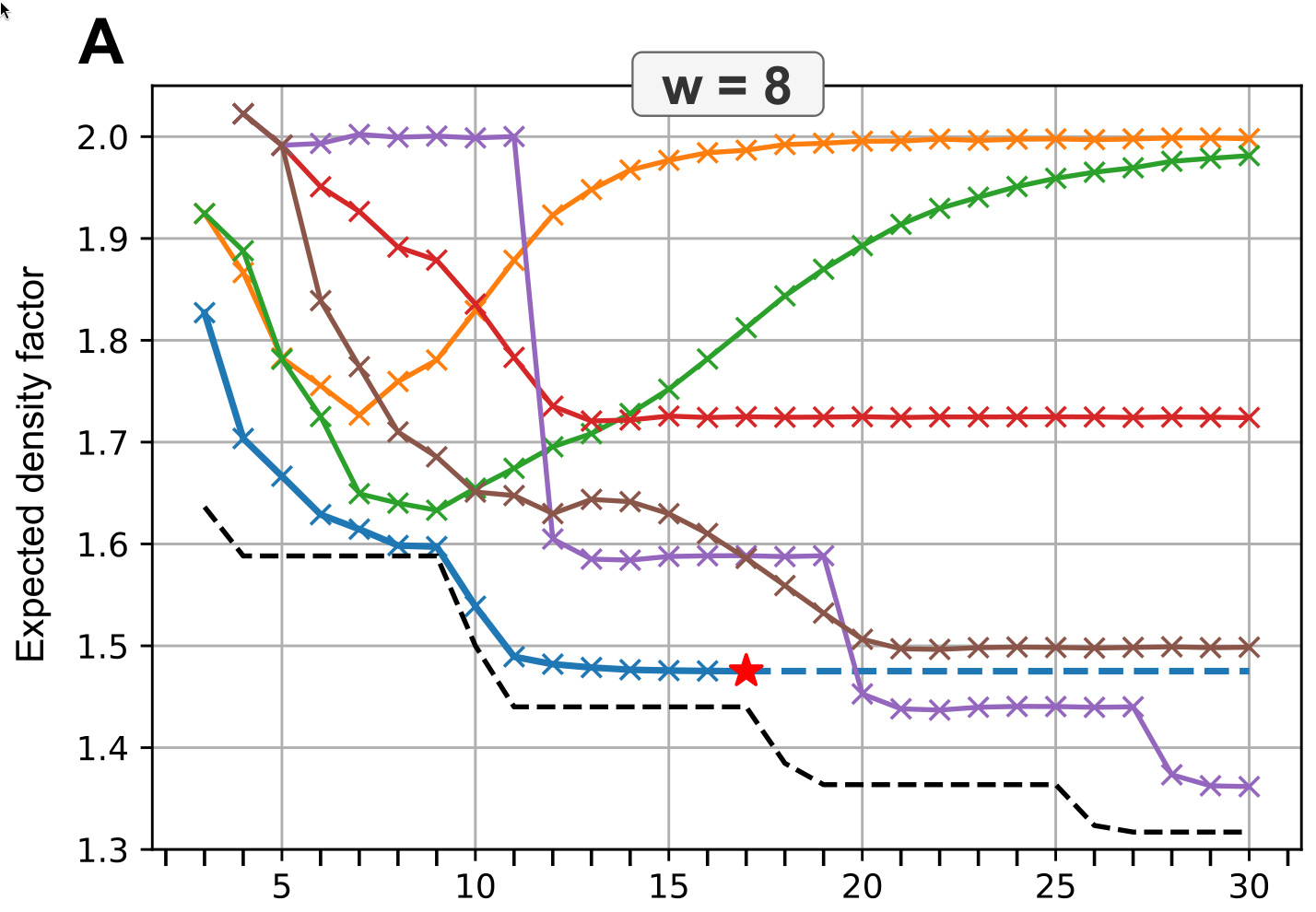
2.6. Minimizer density lower bound

• Density of minimizer scheme is \(\geq 1/\sigma^k\):

  sample exactly every AAA k-mer, and nothing else.

• \(k=1\): density at least \(1/\sigma = 1/4\).

3. Sampling schemes: more general

• Any function \(f: \Sigma^{w+k-1} \to \{0, \dots, w-1\}\)
• We fix \(k=1\) from now: \(f: \Sigma^w\to \{0, \dots, w-1\}\)

3.1. Bidirectional anchors

• Pick the start of the smallest rotation
  • E​A​DCAE......
  • .​A​DCAEB.....
  • ..DC​A​EBE....
  • ...C​A​EBEC...
  • ....​A​EBECD..
  • .....E​B​ECDC.
  • ......​B​ECDCD

3.2. Limitations of bd-anchors

• Lexicographic is bad:
  • A​AAABCD...
  • .​A​AABCDE..
  • ..​A​ABCDEF.
  • ...​A​BCDEFG
• Comparing rotations is unstable:
  • ​A​ABACD..
  • .ABACD​A​.
  • ..B​A​CDAE
• Avoid last \(r\) positions.

3.3. Bd-anchor density for \(k=1\)

4. Smallest-unique-substring anchors

• Idea: instead of smallest rotation: smallest suffix.
• What about CABA: is ABA or A smaller?
  • We choose ABA smaller for stability.
• AB is the smallest unique substring.
• Stable:
  • ​AA​BACD..
  • .​AB​ACDA.
  • ..B​AC​DAE

4.1. Sus-anchor density

4.2. ABB order

• AAAA is BAD:
  • small strings overlap
  • small strings cluster
• We want the opposite!

• ABB order:

  A followed by many non-A is smallest: ABBBBBBBBB

  • no overlap
  • no clustering

4.3. Sus-anchor, ABB order

4.4. Anti-lex

• Anti-lexicographic order:

  A small, followed by largest possible suffix: AZZZZZ is minimal

  • no overlap
  • no clustering

4.5. Sus-anchor, anti-lex order

5. Understanding the lower bound

• To reach lower bound: exactly 2 samples in every \(w+1\) cycle.

5.1. Failure mode

0010101 cycle:

• ​00​1010......
• .​01010​1.....
• ..1​0101​0....
• ...0101​00​...
• ....101​00​1..
• .....01​00​10.
• ......1​00​101
• The 01010 sus is not overlap free
  • Just like how AAA is not overlap free

Goal: find two non-overlapping substrings.

5.2. Can we design a perfectly optimal scheme?

• Goal:

  For every \(w+1\) window, find two non-overlapping small strings.

• Instead of 011...11, search 00...0011...11
  • Also non-overlapping, and more signal.
  • Still not optimal.
• Tried many things. No general solution found yet.

6. Thanks to my co-authors!

• Giulio Ermanno Pibiri
• Bryce Kille
• Daniel Liu
• Igor Martayan

Slides: curiouscoding.nl/slides/minimizers.html

Blog curiouscoding.nl/slides/minimizers